Frequently Asked Questions
Software & Data Processing
The deep SBE41 and SBE61 use the same pressure sensor – a 7000dbar Kistler. And, they are calibrated with the same Paroscientific Digiquartz reference. However, the calibration process is different. A deep SBE41 receives a 2-point sensor only temperature compensation for pressure. The initial accuracy for a deep 41 is +/- 7dbar, typical stability is 2dbar/year. A 61 receives a 4-point temperature compensation for pressure after the instrument is completely assembled, such that the correction includes both the sensor and the electronic boards. The initial accuracy for a 61 is +/-4.5dbar, typical stability is 0.8dbar/year.
The menu to configure the factory parameters you are asking about is accessible through the i*? command. The ? argument for this command will give you a list of all of the arguments to change each individual menu. Let me know if you have any questions about the list of commands in the help menu, and I can try to clarify.
Some cautionary suggestions about changing these parameters:
(1) These parameters should only be changed prior to deployment. Changing them post-deployment could cause you to permanently lose your ability to communicate with the float remotely.
(2) In order to retain Sea-bird Navis warranty coverage, you must provide a log of pre-deployment testing that includes telemetry to your server system after all parameter updates have been performed.
Unfortunately, users cannot currently program their SUNA to start at a preferred time. As soon as the SUNA is powered, the instrument will begin it’s programmed sampling mode on the hour. Users can use the offset feature to change the start time. For example, an offset value of 300 (5 min) changes the start time by five minutes, for example, from 06:00 to 06:05.
The continuous mode setting allows the user to program their SUNA to run continuously for an indefinite amount of time. When power is supplied to the SUNA, it will start data acquisition without an end time or maximum number of frames to measure. In general, we do not recommend this mode for long periods of time because the lamp of the SUNA can burn out. As a general rule of thumb, the SUNA lamp should be replaced when it reaches 750 hours.
The fixed time mode setting allows the user to program their SUNA to run continuously for a period of time or specified number of frames. When data acquisition has completed, the sensor will enter a low-power standby mode.
The periodic mode setting allows the user to select how often, and how long sample intervals are based on frame-based or time-based operation.
For example, if a user would like to program their SUNA to sample every two hours, they would use a sample interval of two hours.
The user would then select either frame-based or time-based operation
For frame-based operation, the user selects the number of light frames the SUNA will sample for.
For time-based operation the user selects how many seconds of light frames the SUNA will sample for.
When the SUNA is powered, the instrument will begin it’s programmed sampling mode on the hour. Users can use the offset feature to change the start time. For example, an offset value of 300 (5 min) changes the start time by five minutes, for example, from 06:00 p.m. to 06:05 p.m.
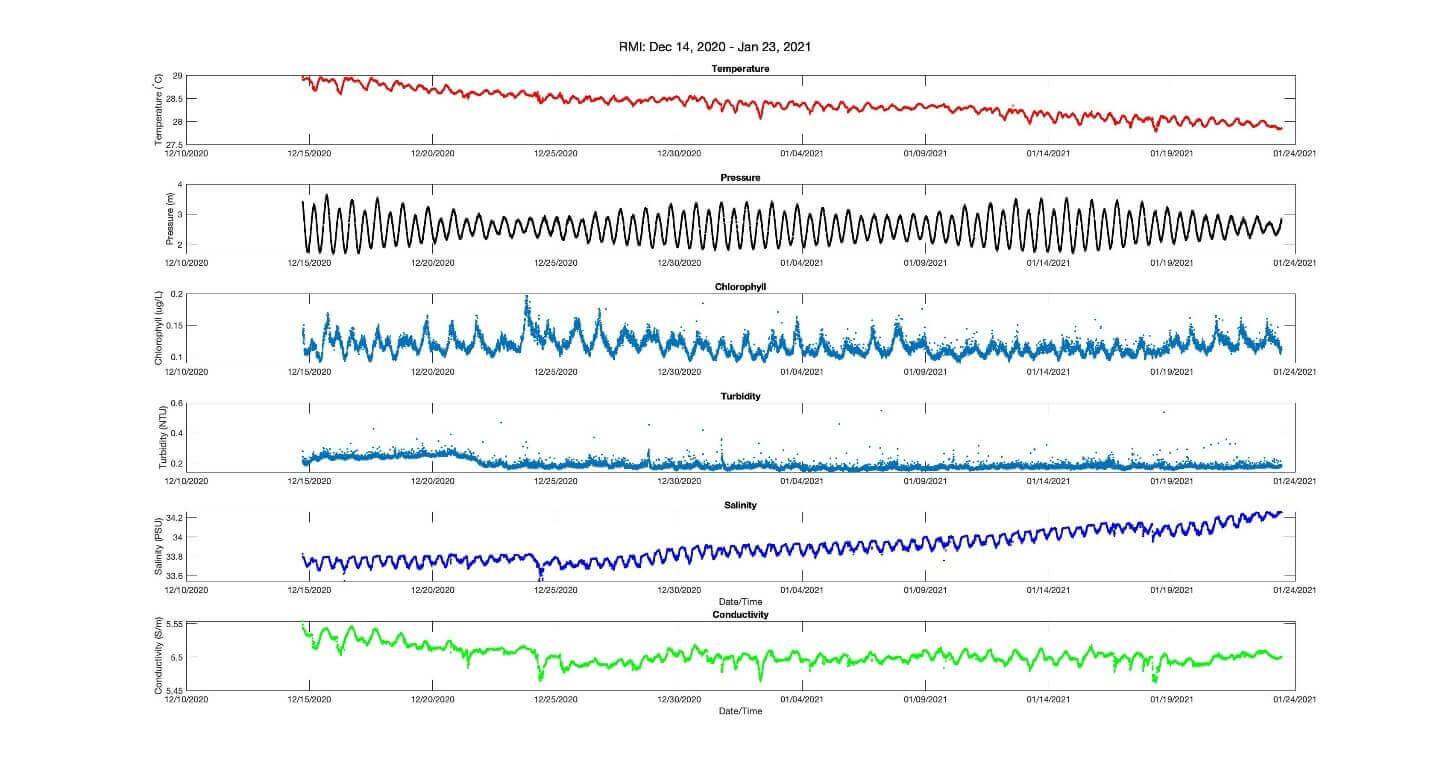
Temperature and Conductivity are two of the most important values taken into consideration when our instrument calculates the practical salinity of seawater. When one sees a change in a measured value, such as temperature, that change will affect your salinity reading in a predictable way, assuming all else is equal. For instance, in an environment where temperature has begun to drift downward you will see a resulting drift of salinity towards being saltier.
Proper cleaning procedures, allowing your CTD to equilibrate at the surface before a profile, updating your calibrations yearly, and bio-fouling prevention are some ways that you can ensure that your instrument will provide accurate salinity data.
For a more comprehensive look at our salinity calculations please refer to App Note 14, which is hosted on our website.
The back-scattering measurements are a portion of the total beam attenuation coefficient of the water being sampled. The beam attenuation is measured during the back-scattering calibration. Therefore, the range specification on the data sheet for the BB sensor (0 – 3 or 0 – 5 m^-1) refers to the beam attenuation coefficient range of the calibration.
There is a note on the data sheet that further explains the backscattering specification:
*Backscattering specifications are given in beam cp (m^-1) based on the regression of the response of the instrument relative to the beam cp measured at the coincident wavelength using an ac-s spectrophotometer. Scale factors for backscattering incorporate the target weighting function and the solid angle subtended.
How can I use Bottle Summary to output the bottle number as well as the trip order to a .btl file?
Yes, it is possible to include bottle ‘serial numbers’ through the use of a .sn file, which is a user-created file containing information about the bottles you have fired. Creating the file before processing your data in Seabird Data Processing’s Bottle Summary module is necessary for the process to work. If a .sn file (same name as input data file, with .sn extension) is found in the input file directory, bottle serial numbers are inserted between the bottle position and date/time columns in the .btl file output.
The format for the .sn file is:
Bottle position, serial number (with a comma separating the two fields)
Cells that have been contaminated with foreign material generally read low of the actual conductivity. Your zero (in air) conductivity reading is generally unaffected.
The conductivity error due to fouling will generally be proportional to the conductivity value. Conductivity is corrected not as an offset but as a ratio (multiplicative) error compared to a reference.
Salinity is a derivative measurement of temperature, conductivity, and pressure, and should be corrected by adjusting the component measurements. Generally speaking, an error in the conductivity measurement will correlate to a directly proportional error in the salinity measurement.
The temperature and salinity correction for the SUNA can be traced to the experiment outlined in Sakamoto et al. 2009, which is the T/S correction our UCI-based SUNA software uses in post-processing only.
Absorption of UV light in seawater is dominated by dissolved nitrate and bromide ions at wavelengths less than 240 nm. To estimate nitrate, it is necessary to remove the absorption due to bromide. The salinity correction addresses the sea salt extinction coefficients due to bromide. In the real ocean, bromide covaries with NaCl. So, during calibration, we can measure the the bromide absorption due to seawater at one salinity and later predict the absorption due to seawater at any salinity.
Artifical seawater surrogates do not necessarily have the correct bromide absorption to be able to validate the the Sakamoto et al. 2009 salinity correction, so the salinity correction may not product accurate results if your data was not collected in natural seawater.
This modification allows the SBE9plus CTD to accept an RS-232C serial instrument data stream and transmit to the surface.
The acceptable baud rate at the SBE9plus CTD is determined by the EPROM version installed in the modem board. These modem board options include, 9600 or 19200 baud, 8 bit data, and “none” parity. At the surface the SBE11 deck unit will extract the serial data from the standard telemetry and transmit data to a remote host PC/computer via a DB-9 connector on the back panel of the deck unit. This data is transmitted to the host computer at 19200 baud regardless of the serial instrument baud rate at the underwater unit.
The SBE 911plus system was designed with idea that all 9plus would operate with all 11plus deck units. With the modification for serial uplink, however, only a modified 9plus will work with a modified 11plus.
The detector wiring is damaged, especially if the LED’s are still flashing. NOTE: CDOM channels do not have visible LED’s, so, do NOT look into the CDOM LED port to confirm its operation (!!).
The ECO firmware is programmed to output an unchanging “floor” value of output counts, if there is no signal from the detector.
Conversely, if the LED is burned out, one would see a changing serial output count, dithering around the ECO dark count value or showing another ambient light condition/change (i.e. values would be changing 48, 51, 47, 52, etc…).
Whether the tau correction is applied depends on where the system is being deployed.
If the system is to be used in shallow, coastal waters where large vertical gradients that change quickly are expected, the tau correction should be applied, as it accounts for the response time and puts the interface between two different water masses in the right place.
If the system is to be used in deep water (>200 m) where the vertical gradients are small, the tau correction should be turned off – in areas where the gradients are small, the calculation adds more noise.
The measurement range and accuracy of the SBE43 are not definite in discrete units (mL/L, mg/L, µMol/L, etc.) Rather, the range and accuracy specification are expressed as a ratio of the calculated oxygen saturation point. This saturation value depends on the temperature and salinity of the water, decreasing in higher temperatures and higher salinities.
The lower limit of detection of dissolved oxygen concentration is going to be constrained by the accuracy specification, which is a ratio of the calculated oxygen saturation (initial accuracy: +/- 2% of saturation). This saturation value varies depending on the temperature and salinity of the water. Common oxygen saturation values in seawater are in the range of 4-7 mL/L. Using this value as an estimate, you can extrapolate that the accuracy of the sensor in many conditions can be as low as +/- 0.1 mL/L. Therefore, the close you get to zero oxygen concentration, the closer the resolution of your measurement will be to the accuracy spec, until you get below 0.1 – 0.2 mL/L and your measured value is smaller than the nominal error margin.
While the theoretical lower limit of the instrument’s measurement range is zero, the measurement becomes less meaningful the closer your dissolved oxygen measurement gets to 2% of the calculated saturation. For example, if you were in an environment where the oxygen saturation was 7 mL/L but the oxygen concentration measured by the SBE43 was 0.28 mL/L, then your accuracy would effectively be +/- 50% of the measurement.
The command interface is different and not inter-compatible for both devices. The sampling and configuration commands are also not inter-compatible. Because of this, they require different software (i.e. SeaFETCom for V1, UCI for V2).
The SeaFET/SeapHOx V1 has native USB compatibility, while the V2 is an RS-232 only device. The V2 requires a USB-to-RS-232 adaptor to connect to a USB port.
The magnetic switch serves different functions on a V1 versus a V2. The V1 uses it to activate & deactivate the internal batteries, but the V2 uses it to provide sample status.
Oftentimes one will see data in their cast that looks erroneous or out of spec, but reviewing the timeline of each cast and the events which transpired can explain these jumps. If you are starting your cast while your CTD is on deck then the time during which the unit is running in air can be spikey or erratic, but this should be solved after the unit has been fully submerged and the pump has activated. The pump on time setting controls how fast the system will turn on the pump after deployment, so filtering out your deckside data can be done by calculating the number of scans to exclude using your pump on time setting, samples to average setting, and native sampling rate of your CTD.
Bubbles in the flow line can also cause spikes in your data towards the start of your deployment if the system isn’t able to normalize at the surface. We typically recommend units stay near the surface for 2-5 minutes in order to allow air bubbles to escape.
Finally, for additional resources in troubleshooting and smoothing data outliers for your CTD data, refer to our documentation on Seabird University.
Data is stored in a RAM page buffer, which is only written to FLASH when it is full. If the instrument is powered off, samples stored in the partially filled page buffer will be lost BUT the recorded sample number will still be the same. This means that when all samples are uploaded, the last few will be unreliable. The page buffer is 256 bytes. If a sample is 17 bytes then up to 15 samples at the end could be lost.
Our suggestion for how to avoid this problem is that if you want every sample, upload data without power cycling the instrument. Otherwise, plan to log samples for N more than you want to acquire, where N is based on the number of samples required to fill the page buffer.
There are other potential causes, but this is more probable. If this method does not resolve your issue, please contact Technical Support.
When the SeapHOx system loses connection with its 37 SMP-ODO CTD component, the system will report back the measured AND derived values related to that instrument as NAN. As part of this, it will also report its External pH as NaN as the salinity correction is missing the CTD’s input. The external pH requires the CTD’s temperature and salinity input in order to make a valid measurement.
The CTD data- the temperature, pressure, oxygen, and salinity come through this Y cable connection. Check to see if your CTD has lost power (either external SeaFET power or internal lithium AA cells) and stopped transmitting data to the SeaFET. If both the CTD and SeaFET are working the next most likely point of failure is the connection between the two units, primarily due to either an incorrect setup of the communication settings or due to a physical loss of connection.
Inspect your connection for signs of a bad cable, bent or loose pins on your bulkhead connector, or water ingress. For the settings side, refer to the manual and integration guide for the correct settings.
Sea-Bird hosts an FTP (file transfer protocol) site for larger data transfers than are available by standard email. The instructions for gaining access to this FTP site can be provided by Sea-Bird Technical Support upon request. Software that is either no longer provided with new instruments (SunaCOM, for instance) or older versions of software can be found in the associated software folder, though we recommend you try the latest version of any software available on our website.
The spike seen in the pump out phase is due to the commencement of flow and reagents/material that is outside the optical path initially but is swept through the optical path during flush out. The spike is accepted as normal behavior of the system and does not affect data quality.
Whether the tau correction is applied depends on where the system is being deployed.nnIf the system is to be used in shallow, coastal waters where large vertical gradients that change quickly are expected, the tau correction should be applied, as it accounts for the response time and puts the interface between two different water masses in the right place.nnIf the system is to be used in deep water (>200 m) where the vertical gradients are small, the tau correction should be turned off – in areas where the gradients are small, the calculation adds more noise.
CAPO4 is the phosphate concentration that the instrument reports as its measurement. CAPO4 is the calculated concentration of an ambient sample using the CAS slope, where CAS is the manufacturer’s scale factor, which is provided by Sea-Bird. nnVAPO4 is used in a QC process to monitor potential drift or spot pump failures or other mechanical problems. VAPO4 is the calculated concentration of an ambient sample using the VAS slope, where VAS is a variable slope calculated in-situ using the on board standard. VAS is only calculated during the Cal Spike frequency runs, used on subsequent samples between the Cal Spike. So, VAS and VAPO4 are not always good values and can affect whole groups of samples between the Cal Spike runs.nnThe calibration for CAPO4 does not include a variable ambient sample of unknown quantity as VAPO4 does.
A setup file is used by Seasave V7, and by each module in SBE Data Processing, to remember the way you had the program set up. You can save the file to a desired filename and location, and then use it when you run the software the next time, to ensure that the software will be set up the same way:
- A .psa file is created by Seasave V7 to store program settings, such as the instrument configuration (.con or .xmlcon) file name and path, serial ports, water sampler, TCP/IP ports, serial data output, etc. as well as size, placement, and setup for each display window.
- A .psa file is created by each module in SBE Data Processing to store program settings, such as the input filename and path, output filename, and module-specific parameters (for example, for Data Conversion: variables to convert, ascii or binary output, etc.).
If you want to set up real-time acquisition or data processing on more than one computer in the same way, simply copy the file for the desired setup, and transfer it to the other computer via your network, email, a thumb drive, or some other media. Then, after you open the software on the second computer, select the setup file you want to use.
- Seasave V7: Select File / Open Setup File.
- SBE Data Processing: In the module dialog box, on the File Setup tab, click the Open button under Program setup file.
Sea-Bird’s main software package is called Seasoft©.
- Seasoft V2 — Seasoft V2 is actually a suite of stand-alone programs. You can install the entire suite or just the desired program(s).
- Deployment Endurance Calculator — calculates deployment length for moored instruments, based on user-input deployment scheme, instrument power requirements, and battery capacity.
- SeatermV2 — terminal program launcher that interfaces with Sea-Bird instruments developed or redesigned in 2006 and later, which can output data in XML. Can be used with SBE 16plus V2, 16plus-IM V2, 19plus V2, 25plus, 37 (SI, SIP, SM, SMP, IM, IMP, all with firmware 3.0 and later), 37 with oxygen (SIP-IDO, SIP-ODO, SMP-IDO, SMP-ODO, IMP-IDO, IMP-ODO), 39plus, 54 and PN 90588, 56, 63, and Glider Payload CTD. SeatermV2 provides setup, data retrieval, and diagnostic tests.
- Seaterm — terminal program that interfaces with most older Sea-Bird instruments, providing setup, data retrieval, and diagnostic tests.
- SeatermAF — terminal program that interfaces with instruments that provides auto-fire capability for autonomous operation of an SBE 32 Carousel Water Sampler (with an SBE 17plus V2 or AFM) or SBE 55 ECO Water Sampler, providing setup, data retrieval, and diagnostic tests.
- Seasave V7 — acquires, converts, and displays real-time or archived data. Seasave V7 is an entirely new version of Seasave, officially released March 2007.
- SBE Data Processing — converts, edits, processes, and plots data; some of SBE Data Processing’s most commonly used modules include Data Conversion, Bottle Summary, Align CTD, Bin Average, Derive, Cell Thermal Mass, Filter, and Sea Plot.
- Plot39 — plots ASCII data that has been uploaded from SBE 39plus, 39, or 39-IM Temperature Recorder or SBE 48 Hull Temperature Sensor.
- Seasoft for Waves —
Provides setup, data retrieval, data processing, auto-spectrum and time series analysis, statistics reporting, and plotting for the SBE 26 and SBE 26plus Seagauge Wave & Tide Recorder. Also provides setup, data retrieval, data processing, and plotting for the SBE 53 BPR Bottom Pressure Recorder.
Additional software is available to simplify use of coastal instruments:
- Universal Coastal Interface (UCI) —
Provides setup, operation, in-field reference checks, data upload, and plotting for the HydroCAT, HydroCAT-EP, and SUNA.
First off, let’s see what a relatively good Raw Data Plot looks like.
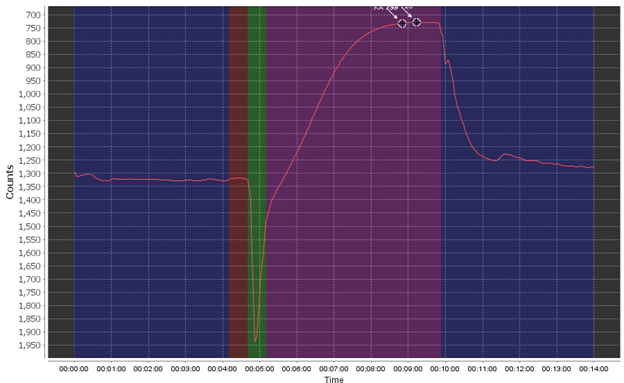
The different phases are the pre-flush phase (dark blue), the ambient baseline reading period (red), the sample reagent pump phase (green), the sample read/reaction phase (purple), and finally the post-flush phase (dark blue). During a “spiked run” the full set of phases are repeated twice.
Using this as an example, you want to see a flat pre- and post-pump phase, a stable (flat) ambient read phase, and a pronounced smooth reaction curve. You may see small bumps here and there due to very small bubbles or other effects but this can be negligible.
The most common failure mode is the bubble spike flag, which triggers when air is introduced into the system, most commonly through the sample line but possibly through incorrectly installed cartridges or tubing.
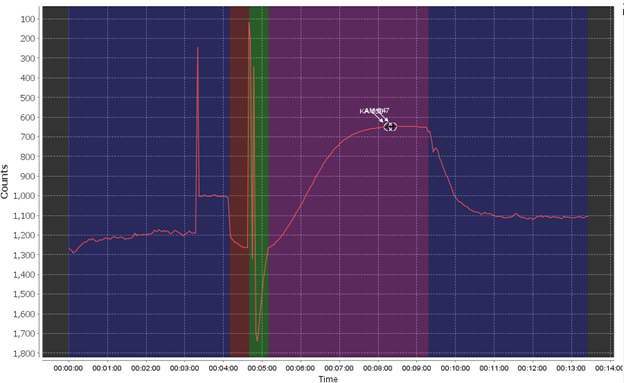
The bubble failure is typically identified by large jumps and spikes randomly in the data, primarily in the pre- and post- pump phase and the ambient read phase. Air bubbles create an unstable base line (red) which will affect the sensor’s accuracy. In extreme examples it can completely overshadow the reaction curve as well or shift the baseline to the point where your reaction creates a negative value. Air bubbles often exacerbate other issues, like weak pumps, clogged filters, or already low phosphate in your sample.
Since bubbles can come from a few different places there are multiple checks you can do to try to stop bubbles from appearing in your data. The most important check is ensuring that your hydrocycle is fully submerged for the entirety of your deployment, as the sample line being exposed to air will introduce bubbles.
You should check that each of your reagent carts are fully installed. Press down on each reagent cart until you can hear them click and be careful about applying too much force to any of the plastic pieces that may crack and allow for leaks or air.
You can also test the pump volumes of each reagent and sample to see if your filters are clogged or if there is another issue causing the sample injection system to fail, like a leak. You do so by using Cyclehost’s Pump controls. You should choose all pumps and run each for 100 pumps. A healthy system will pump 1-1.3 ml of reagent and 2.5-3 ml of sample.
If you have bubbles already and need to recover, the most thorough method is to follow our maintenance and cleaning instructions in the manual, primarily the extended flush. Running the extended flush multiple times should be enough to clear bubbles from your system if no other issues are evident.
If doing so still fails to recover your instrument’s counts please reach out to technical support with a copy of your hydrocycle data and brief timeline of events.
For best performance and compatibility, Sea-Bird recommends that customers set their computer to English language format and the use of a period (.) for the decimal symbol. Some customers have found corrupted data when using the software’s binary upload capability while set to other languages.
To update your computer’s language and decimal symbol (instructions are for a Windows 7 operating system):
- In the computer Control Panel window, select Region and Language.
- In the Region and Language window, on the Formats tab, select English in the Format pull down box.
- In the Region and Language window, click the Additional settings . . . button. In the Customize Format window, select the period (.) in the Decimal symbol pull down box, and click OK.
- In the Region and Language window, click OK.
No. An ISUS V2 does not have the correct hardware to be used with ISUSCom. If you have an ISUS V2, and wish to use it with this software, please contact Sea-Bird Scientific Customer Support to discuss upgrading your ISUS.
By default the clock of the StorX is set to UTC time rather than local time.
The StorX will add a UTC timestamp to each data frame that it collects.
The schedule.txt file on board the StorX is a daily schedule, and represents a 24 hour period (00:00 to 24:00). The schedule assumes that the StorX is set to UTC time. The StorX is set to use UTC time by default.
Note that this is especially important if you have a different instrument scheduling for day light hours versus nighttime.
You can check your StorX clock by connecting through the serial connection and using a serial terminal emulator such as hyper-terminal:
First, connect to the StorX serial port, to obtain a command prompt.
From the C:\ prompt, you can verify the StorX clock time by typing “clock get”.
Verify that the date and time provided is correct in UTC time.
If the date and time requires updating, you will first have to use the “date” command to set the PicoDOS time to the correct time in UTC.
Once the PicoDOS time is set correctly, you can then enter a “clock set” command to send the PicoDOS time to the StorX clock.
Be sure to type “clock get” again to verify the time is now correct.
This should be done if the system is not used for some time or performed before a deployment.
Can I install my Sea-Bird CD-ROM on multiple computers or give it to another interested scientist?
You are free to install the software on multiple computers and to give the software to any interested potential user.
Sea-Bird’s Seasoft© software is provided free of charge to Sea-Bird users and is not subject to any license. Seasoft is protected by copyright laws and international copyright treaties, as well as other intellectual property laws and treaties. All title and copyrights in and to Seasoft and the accompanying printed materials, and any copies of Seasoft, are owned by Sea-Bird Electronics. There are no restrictions on its use or distribution, provided such use does not infringe on our copyright.
The software is offered as a download here.
You can plot the raw data from a .dat or .hex file with Seasave V7.
Once the data is converted to a .cnv file with engineering units (using SBE Data Processing’s Data Conversion), you can plot the data in SBE Data Processing’s Sea Plot.
-
Because Sea Plot only works with archived files, it is more sophisticated than Seasave. For example, Sea Plot can provide multiple file overlays, waterfall plots, and TS plots with contours.
If you wish to view the actual numbers you can open the .cnv file (if it was converted as ASCII) with any word processor or text editor.
The configuration file defines the instrument — auxiliary sensors integrated with the instrument, and channels, serial numbers, and calibration dates and coefficients for all the integrated sensors (conductivity, temperature, and pressure as well as auxiliary sensors). Sea-Bird’s real-time acquisition and data processing software uses the information in the configuration file to interpret and process the raw data (sensor frequencies and voltages). If the configuration file does not match the actual instrument configuration, the software will not be able to interpret and process the data correctly.
When Sea-Bird ships a new instrument, we include a .con or .xmlcon file that reflects the current instrument configuration. The file is named with the instrument serial number, followed with the .con or .xmlcon extension. For example, for an instrument with serial number 2375, Sea-Bird names the .xmlcon file 2375.xmlcon. You may rename the configuration file if desired; this will not affect the results.
(Click here to see an example of where to find the serial number on your instrument)
Seasave V7 and SBE Data Processing version 7.20 (2009) introduced .xmlcon files (in XML format). Versions 7.20 and later allow you to open a .con or .xmlcon file, and to save it to a .con or .xmlcon file.
To view or modify the configuration file, use the Configure Inputs menu in Seasave V7, or the Configure menu in SBE Data Processing.
Notes:
- Seasave V7 and SBE Data Processing check that the serial number in the configuration file matches the instrument serial number in the .dat or .hex data file. If they are not the same, you will get an error message. The instrument serial number can be verified by sending the Status command (DS or #iiDS, as applicable) in the appropriate terminal program.
- SBE 16, 16plus, 16plus-IM, 16plus V2, 16plus-IM V2, 19, 19plus, 19plus V2, 21, and 49 — The instrument serial number is the same as the serial number of both the conductivity and temperature sensors.
- SBE 37 (older), 39, 39plus, and 48 — These instruments store calibration coefficients internally and do not accept auxiliary sensors, so they do not have configuration files.
- SBE 37 (newer) that is compatible with SeatermV2 terminal program — SeatermV2 creates a configuration file for these instruments when it uploads data. The configuration file can then be used for processing the data in SBE Data Processing.
- The calibration date in the configuration file is for information only. It does not affect the data processing.
- When Sea-Bird recalibrates an instrument, we ship the instrument with a Calibration Sheet showing the new calibration coefficients (1 calibration sheet per sensor on the instrument that was calibrated). Sea-Bird also supplies a .xml file with the calibration coefficients for each calibrated sensor. The .xml files can be imported into Seasave or SBE Data Processing, to update the calibration coefficients in the configuration file.
— For CTDs: Sea-Bird also creates a new configuration file, which includes calibration coefficients for the CTD as well as any auxiliary sensors that were returned to Sea-Bird with the CTD. If you did not return the auxiliary sensors with the CTD, you need to update the configuration file to include information on the auxiliary sensors that you plan to deploy with your CTD.
A .psa (program setup) file is used by Seasave V7 and by each module in SBE Data Processing to remember the way you had the program set up. You can save the .psa file to a desired filename and location, and then use it when you run the software the next time, to ensure that the software will be set up the same way:
- A .psa file is created by Seasave V7 to store program settings, such as the instrument configuration (.con or .xmlcon) file name and path, serial ports, water sampler, TCP/IP ports, serial data output, etc. as well as size, placement, and setup for each display window.
- A .psa file is created by each module in SBE Data Processing to store program settings, such as the input filename and path, output filename, and module-specific parameters (for example, for Data Conversion: variables to convert, ascii or binary output, etc.).
If you want to set up real-time acquisition or data processing on more than one computer in the same way, simply copy the .psa file for the desired setup, and transfer it to the other computer via your network, email, a CD-ROM, or some other media. Then, after you open the software on the second computer, select the .psa file you want to use.
- Seasave V7: Select File / Open Setup File.
- SBE Data Processing: In the module dialog box, on the File Setup tab, click the Open button under Program setup file.
MatLab can import flat ASCII files. To produce those files:
- Run SBE Data Processing’s Data Conversion module to produce a .cnv file with data in ASCII engineering units from the raw data file. This file also contains header information.
- Run SBE Data Processing’s ASCII Out module to remove the header information, outputting just the data portion of the converted data file to a .asc file. Optionally, you can also output the header information to a .hdr file.
Current Sea-Bird software was designed to work on a PC running Windows 7/8/10 (both 32-bit and 64-bit). Sea-Bird provides the software free of charge as part of our instrument support. Because of this, we do not have the resources to write and provide support software for other operating systems, such as Apple, Unix, or Linux.
- If you have a valid PC emulator on your system, the Sea-Bird software may run, but we have no way to confirm this, or that the I/O connections to the instrument will properly function.
- If you have access to a PC running Windows, you can use Sea-Bird’s software to convert the data from our proprietary format to ASCII (in engineering units of C, T, P, etc. with calibration coefficients applied); then you could use your own software on a different computer to perform additional processing.
The flag variable column is added by Data Conversion (if you process data using Sea-Bird software) or ASCII In (if you are importing data that was generated using other software). The Loop Edit module sets the flag variable to bad for scans that show a pressure slowdown or reversal. The flag variable is then used by the rest of the SBE Data Processing modules as an indication of a bad scan, allowing you to exclude scans that are marked bad from processing performed in a module, if desired.
Initially all scans are marked good (flag value of 0) in Data Conversion or ASCII In. A flag of -9.99e-29 indicates the scan has been marked bad by Loop Edit.
Note: All occurrences of the bad value (-9.99e-29) can be replaced with a different value in ASCII Out. This may be useful for plotting purposes, as -9.99e-29 looks like 0 in a data plot.
How does Sea-Bird software calculate conductivity, temperature, and pressure in engineering units?
For formulas for the calculation of conductivity, temperature, and pressure from the raw data, see the calibration sheets for your instrument. If you cannot find the calibration sheets, contact us with your instrument serial number (Click here to see an example of where to find the serial number on your instrument).
The Seasave and SBE Data Processing manuals document the derived variable formulas in an Appendix (Derived Parameter Formulas). The Help files for these programs also document the formulas.<!-- To download the software and/or manuals, go to Software-->.
The formulas are provided in Application Note 69: Conversion of Pressure to Depth.
In Seasoft-DOS version 4.249 and higher (March 2001 and later), January 1 is Julian Day 1. Therefore, noon on January 1 is Julian Day 1.5. Earlier versions of the software incorrectly defined January 1 as Julian Day 0, so noon on January 1 would appear as Julian Day 0.5.
All release versions of SBE Data Processing correctly identify January 1 as Julian Day 1.
Seasoft V2’s Seasave (older software, replaced with Seasave V7 in 2007) created a .dat file from data acquired from the SBE 11plus V2 Deck Unit / SBE 9plus CTD. This also applies to earlier versions of the Deck Unit and CTD.
Some text editing programs modify the file in ways that are not visible to the user (such as adding or removing carriage returns and line feeds), but that corrupt the format and prevent further processing by Seasoft. Therefore, we strongly recommend that you first convert the data to a .cnv file (using SBE Data Processing’s Data Conversion module), and then use other SBE Data Processing modules to edit the .cnv file as desired.
Sea-Bird is not aware of a technique for editing a .dat file that will not corrupt it.
Sea-Bird distributes a utility program, Fixdat, that may repair a corrupted .dat file. Fixdat.exe is installed with, and located in the same directory as, SBE Data Processing.
Note: Seasave V7 creates a .hex file instead of a .dat file from data acquired from the SBE 11plus V2 Deck Unit / SBE 9plus CTD. See the FAQ on editing a .hex file.
Some text editing programs modify the file in ways that are not visible to the user (such as adding or removing carriage returns and line feeds), but that corrupt the format and prevent further processing by Seasoft. Therefore, we strongly recommend that you first convert the data to a .cnv file (using SBE Data Processing’s Data Conversion module), and then use other SBE Data Processing modules to edit the .cnv file as desired.
However, if you still want to edit the raw data, this procedure provides details on one way to edit a .hex data file with a text editor while retaining the required format. If the editing is not performed using this technique, Seasoft may reject the data file and give you an error message.
- Make a back-up copy of your .hex data file before you begin.
- Run WordPad.
- In the File menu, select Open. The Open dialog box appears. For Files of type, select All Documents (*.*). Browse to the desired .hex data file and click Open.
- Edit the file as desired, inserting any new header lines after the System Upload Time line. Note that all header lines must begin with an asterisk (*), and *END* indicates the end of the header. An example is shown below, with the added lines in bold:
* Sea-Bird SBE 21 Data File:
* FileName = C:\Odis\SAT2-ODIS\oct14-19\oc15_99.hex
* Software Version Seasave Win32 v1.10
* Temperature SN = 2366
* Conductivity SN = 2366
* System UpLoad Time = Oct 15 1999 10:57:19
* Testing adding header lines
* Must start with an asterisk
* Can be placed anywhere between System Upload Time and END of header
* NMEA Latitude = 30 59.70 N
* NMEA Longitude = 081 37.93 W
* NMEA UTC (Time) = Oct 15 1999 10:57:19
* Store Lat/Lon Data = Append to Every Scan and Append to .NAV File When is Pressed
** Ship: Sea-Bird
** Cruise: Sea-Bird Header Test
** Station:
** Latitude:
** Longitude:
*END*
-
In the File menu, select Save (not Save As). The following message may display:
You are about to save the document in a Text-Only format, which will remove all formatting. Are you sure you want to do this?
Ignore the message and click Yes. -
In the File menu, select Exit.
This error message typically means that some of the .dll files needed to run the software are installed incorrectly or have been corrupted. We recommend that you remove the software, and then reinstall the latest version.
Note: Use the Windows’ Add or Remove Programs utility to remove the software; do not just delete the .exe file.
The T-C Duct on a 911plus imposes a fixed delay (lag time) between the temperature measurement and the conductivity measurement reported in a given data scan. The delay is due to the time it takes for water to transit from the thermistor to the conductivity cell, and is determined by flow rate (pump rate). The average flow rate for a 9plus is about 30 ml/sec. The Deck Unit (11plus) automatically advances conductivity (moves it forward in time relative to temperature) on the fly by a user-programmable amount (default value of 0.073 seconds), before the data is logged on your computer. This default value is about right for a typical 9plus flow rate. Any fine-tuning adjustments to this advance are determined by looking for salinity spikes corresponding to sharp temperature steps in the profile and, via the SBE Data Processing module Align CTD, trying different additions (+ or -) to the 0.073 seconds applied by the Deck Unit, until the spikes are minimized. Having found this optimum advance for your CTD (corresponding to its particular flow rate), you can use that value for all future casts (change the value in the Deck Unit) unless the CTD plumbing (hence flow rate) is changed.
Oxygen and other parameters from pumped sensors in the same flow as the CT sensors can also be re-aligned in time relative to temperature, to account for the transit time of water through the plumbing. A typical plumbing delay for the SBE 43 DO Sensor is 2 seconds. However, the DO sensor time constant varies from approximately 2 seconds at 25 °C to 5 seconds at 0 °C. So, you should add some advance time for this as well (total delay = plumbing delay + response time). As for the conductivity alignment, the Deck Unit can automatically advance oxygen on the fly by a user-programmable amount (default value of 0 seconds) before the data is logged on your computer. However, because there is more variability in the advance, most users choose to do the advance in post-processing, via the SBE Data Processing module Align CTD. For additional information and discussion, refer to Module 9 of our training class and the SBE Data Processing manual.
Note: Alignment values are actually entered in the 11plus Deck Unit and in SBE Data Processing relative to the pressure measurement. For the 9plus, it is sufficiently correct to assume that the temperature measurement is made at the same instant in time and space as the pressure measurement.
Section 3: Typical Data Processing Sequences in the SBE Data Processing manual provides typical data processing sequences for our profiling CTDs, many moored CTDs, and thermosalinographs. Typical values for aligning, filtering, etc. are provided in the sections detailing each module of the software. This information is also documented in the software’s Help file. To download the software and/or manual, click here: SBE Data Processing.
For formulas for the calculation of conductivity, temperature, and pressure from the raw data, see the calibration sheets for your instrument (if you cannot find the calibration sheets, contact us with your instrument serial number at seabird@seabird.com> or +1 425-643-9866).
For derived parameter formulas (salinity, sound velocity, density, etc.), see the Seasave and SBE Data Processing manuals, which document these formulas in an Appendix. Additionally, the formulas are documented in the Help files for these programs.
In July 2015, Sea-Bird released updated software to address intermittent connectivity issues where the host computer or SeatermV2 cannot recognize an instrument communicating via its internal USB connector. Field Service Bulletin 28 describes the problem and the installation of updated software to solve the problem.
Files that are delivered with Sea-Bird Scientific and third party equipment to describe the sensors data output and calibration coefficients come in two types. Calibration files or *.cal files and telemetry definition format files or *.tdf files. In some cases, systems are created that network many sensors together and their combined data is provided in one serial output. The simplest example is a HOCR sensor that generates both light and dark frames. A more complex example is a HPROII profiling system that may contain as many as 5 sensors and 7 individual calibration and tdf files. These files must be used to both collect and process the data. This can become quite confusing to keep track of all these files so Sea-Bird Scientific developed SIP files. All CAL and TDF files required for a system are zipped using winzip and the extension changed from *.ZIP to *.SIP. The file name includes the system description (usually the network master serial number) and the creation date. This SIP file can then be used in place of individual files to collect and process data.
HOCR sensors output two distinct frame types (light and dark). Thermal dark current changes that occur within the spectrograph are corrected across the full spectrum with the use of a mechanical dark shutter that closes periodically in the radiometer. This creates a unique frame of data that must be collected separately from the light data. SATView requires both calibration files so that it collects both data outputs.
Scientific
The deep SBE41 and SBE61 use the same pressure sensor – a 7000dbar Kistler. And, they are calibrated with the same Paroscientific Digiquartz reference. However, the calibration process is different. A deep SBE41 receives a 2-point sensor only temperature compensation for pressure. The initial accuracy for a deep 41 is +/- 7dbar, typical stability is 2dbar/year. A 61 receives a 4-point temperature compensation for pressure after the instrument is completely assembled, such that the correction includes both the sensor and the electronic boards. The initial accuracy for a 61 is +/-4.5dbar, typical stability is 0.8dbar/year.
The pH sensor will be shipped dry but was pre-conditioned in seawater (generally from Pacific Ocean waters near Hawaii). While conditioning and evaluating the pH sensor, only expose it filtered, sterilized natural seawater. Do not use seawater CRMs (Certified Reference Material), synthetic seawater, deionized water, NaCl Solutions, or tap water.
Before pre-deployment testing, you will need to fill the plumbing around the pH sensor with natural seawater. The pH sensor needs time to acclimate to the ionic concentration of region specific waters. Once wet, the time to recondition the sensor so that it will report within its accuracy specification depends on several factors, including the ionic composition of the seawater used and the amount of time the pH sensor was stored dry. This time can range from several hours to up to three days.
When the seawater bridge between Counter Electrode and ISFET is broken for longer than 10 seconds, it will be necessary to re-condition the sensor. The sensor does not require recalibration after being re-conditioned.
To prepare the sensor for deployment, it is recommended that several days prior to deployment, the isolated battery is connected via the float interface and the pH sensor is stored in water that is similar to the deployment site. The sensor should be stored dry to avoid bio-fouling of the ISFET and the battery may be removed during storage. Seawater creates a half cell bridge between the Counter Electrode and ISFET, and power to that circuit is provided by the isolated 9V cell. Without seawater, the battery is unnecessary and may be disconnected.
Cells that have been contaminated with foreign material generally read low of the actual conductivity. Your zero (in air) conductivity reading is generally unaffected.
The conductivity error due to fouling will generally be proportional to the conductivity value. Conductivity is corrected not as an offset but as a ratio (multiplicative) error compared to a reference.
Salinity is a derivative measurement of temperature, conductivity, and pressure, and should be corrected by adjusting the component measurements. Generally speaking, an error in the conductivity measurement will correlate to a directly proportional error in the salinity measurement.
The temperature and salinity correction for the SUNA can be traced to the experiment outlined in Sakamoto et al. 2009, which is the T/S correction our UCI-based SUNA software uses in post-processing only.
Absorption of UV light in seawater is dominated by dissolved nitrate and bromide ions at wavelengths less than 240 nm. To estimate nitrate, it is necessary to remove the absorption due to bromide. The salinity correction addresses the sea salt extinction coefficients due to bromide. In the real ocean, bromide covaries with NaCl. So, during calibration, we can measure the the bromide absorption due to seawater at one salinity and later predict the absorption due to seawater at any salinity.
Artifical seawater surrogates do not necessarily have the correct bromide absorption to be able to validate the the Sakamoto et al. 2009 salinity correction, so the salinity correction may not product accurate results if your data was not collected in natural seawater.
The SeaFET and SeapHOx systems are designed to sample at a fixed depth. If you want to run discreet samples at depth intervals, you will need to find a way to move the system to a specific depth before each sample interval and stop the descent / ascent for the entire pumping and sampling cycle to get a valid CTD / pH / Oxygen sample.
If you are able to communicate with the system through the serial I/O during profiling, you can send a sampling command to the sensor at each depth point and allow it to complete its sample cycle. Consult the manual for each model for the length of time required to complete each sample. Once the sensor provides a sample, you can then move it to the next depth point and repeat.
If you aren’t running real-time communications to the SeaFET/SeapHOx, you could also set it to autonomously sample at a time interval that gives you enough time to move the package to a new depth point between sample cycles. The challenges with this approach would be to know exactly when the sensor is sampling without any direct feedback from the instrument.
SUNAs ordered with the 5mm path length coupler as a factory option will perform much better in low light transmission waters due to the shorter length the light needs to travel leading to less absorption. Equipping your SUNA with the factory bio-wiper option will also perform better and be less susceptible biofouling or buildup of other material that can reduce light transmission.
There are also some maintenance practices and device settings that can give SUNA a better probability of being able to capture enough light for a sample. Enable adaptive integration will trigger the SUNA to increase the lamp on time when light received by the spectrometer is low. It is also important to clean the windows as frequently as possible and monitor lens for scratches. Finally, you want your maximum light spectral counts at the peak wavelength (around 240nm) to be between 45,000 and 55,000 counts in pure or deionized water. This can be viewed in the “Spectra” tab in UCI when sampling or replaying data. If your peak spectrometer output is below 45,000 counts after cleaning the window, you may increase the integration period by 25 to 50 ms if needed (but not more; further changes require a factory recalibration). After adjusting the integration period, always perform a reference spectrum update per the instructions in the SUNA manual.
The ISFET has two reference electrodes: an internal reference and an external reference, that give separate reference potentials to the ISFET and show separate pH values (pH Internal and pH External). After the corrections for temperature and salinity are applied, the values from the internal and external are similar, and let the user verify the validity of the sensor’s measurements.
Internal reference:
The internal reference electrode inside the DuraFET® is immersed in a bath of saturated potassium chloride (KCl) gel and is physically separated from the environment. The KCl gel exposes the Ag/AgCl internal electrode to a relatively constant chloride concentration. The sensor can therefore measure pH regardless of environmental salinity. If accurate salinity and temperature data are not available, the internal cell is generally more accurate.
External reference:
The external reference electrode has a Ag/AgCl reference electrode in direct contact with seawater. The potential of this electrode varies with pH and chloride concentration, so unless the chloride concentration is known, the external reference is not stable. To correct this, salinity can act as an approximation of chloride concentration. If accurate salinity data is available, it can be applied to the pH external data and significantly reduce measurement errors, and give the most accurate and stable pH data.
Artificial seawater is problematic because the salts in artificial seawater do not completely dissolve leaving you with a solution that does not completely match the ionic concentration of seawater. This is true for synthetic blends (made for aquariums) or ones made from drying natural seawater. The different ionic concentration leads to drift and potential offsets in the pH sensor. This leads to an inaccurate K0 and initial drift in the external reference of the pH sensor, the internal reference electrode should be unaffected because it separated from the seawater by a saturated solution of KCl gel. This occurs because the pH sensor external reference electrode is a solid state AgCl electrode which is in direct contact with the seawater. A unconditioned Ag/Cl external electrode K0 typically changes by 3mV (60mpH) when exposed to natural seawater for the first time. The challenge here is without knowing the ionic composition of the artificial seawater it is difficult to determine exactly how long the drift will occur or if there will be a permanent offset. This is why we recommend to only use natural seawater.
When the Ag/AgCl is first installed in the sensor it is pure Ag/AgCl, but when it is exposed to seawater it reacts with the ions (Br- mostly, but there are other ions too) in seawater which changes its ionic composition and its standard potential. The standard potential is the K0 coefficient which is provided to the customer and the manufacturer the sensors in seawater for ~3 days in natural seawater to ensure the external electrode is conditioned to seawater prior to K0 calibration in seawater baths. If the sensor is then put into artificial seawater with the incorrect ionic compositions, you risk deconditioning the external reference which could lead to inaccurate measurements and drift in the sensor when first deployed. The sensor should recondition to seawater after deployment. The reconditioning can take 3 days to 2 weeks, however permanent offsets can remain even after the external reference has stabilized.
However, if you cannot obtain natural seawater on a regular basis. You could obtain some natural seawater when the pH sensor is recovered or deployed. The seawater could be taken back to your lab, filtered and stored in a dark container in a cool and dark place for a couple months. Just be sure to filter the seawater again before you fill the wet cap to store the pH sensor for long periods of time.
The measurement range and accuracy of the SBE43 are not defined in discrete units (mL/L, mg/L, µMol/L, etc.) Rather, the range and accuracy specification are expressed as a ratio of the calculated oxygen saturation point. This saturation value depends on the temperature and salinity of the water, decreasing in higher temperatures and higher salinities.
The more detailed answer is a theoretical maximum value can be calculated. While the absolute maximum value would need to be calculated using the highest value one could select as a reference saturation point in natural waters, this theoretical maximum value’s calculation is demonstrated below:
10.84 ml/l (15.49 mg/l) the oxygen saturation point for
In the coldest (-2°C) and least saline (0 PSU) water, the oxygen saturation point is 10.84 ml/l (15.49 mg/l. Using this as a reference saturation point, 10.84 ml/l is multiplied by 1.2 to make 13.01 ml/l (18.59 mg/l), or 120% of the oxygen saturation; this represents the upper end of the measurement range in the given water and can be called the theoretical maximum value for the sensor.
The measurement range and accuracy of the SBE43 are not definite in discrete units (mL/L, mg/L, µMol/L, etc.) Rather, the range and accuracy specification are expressed as a ratio of the calculated oxygen saturation point. This saturation value depends on the temperature and salinity of the water, decreasing in higher temperatures and higher salinities.
The lower limit of detection of dissolved oxygen concentration is going to be constrained by the accuracy specification, which is a ratio of the calculated oxygen saturation (initial accuracy: +/- 2% of saturation). This saturation value varies depending on the temperature and salinity of the water. Common oxygen saturation values in seawater are in the range of 4-7 mL/L. Using this value as an estimate, you can extrapolate that the accuracy of the sensor in many conditions can be as low as +/- 0.1 mL/L. Therefore, the close you get to zero oxygen concentration, the closer the resolution of your measurement will be to the accuracy spec, until you get below 0.1 – 0.2 mL/L and your measured value is smaller than the nominal error margin.
While the theoretical lower limit of the instrument’s measurement range is zero, the measurement becomes less meaningful the closer your dissolved oxygen measurement gets to 2% of the calculated saturation. For example, if you were in an environment where the oxygen saturation was 7 mL/L but the oxygen concentration measured by the SBE43 was 0.28 mL/L, then your accuracy would effectively be +/- 50% of the measurement.
The ECO-PAR, due to the nature of PAR sensors, cannot be accurately calibrated outside of the Sea-Bird facility. However, there are some functionality tests that can aid in pre-deployment.
A bright flashlight can validate whether the instrument sees light at all.
On a bench test one should see between 1000-4000 counts normally with the instrument in the white cap standing up on the benchtop. Use a terminal program to see the raw counts, such as Tera Term, and point a flashlight beam near the white cap. Doing so with a functioning unit will cause the counts to go to approximately a couple of thousand in a hair trigger fashion. It should be possible to decrease the counts on a properly functioning instrument by cupping ones hands around the white cap to shield it from light. It should be easy to get a response of a couple of hundred counts total in doing this. In the field if you shine a flashlight beam directly into the optics will see low level ambient light and it is easy to regulate the output in counts at the low end of the range (less than 1000 counts) when it is functioning normally. If your unit is not properly functioning, it will go from 50-ish to a couple of thousand counts and it will be very difficult or impossible to get an output of a couple of hundred counts. While the ranges of the response may differ between PAR models, these tests can be used with other PAR sensors to verify operation.
The ECO-PAR, due to the nature of PAR sensors, cannot be accurately calibrated outside of the Sea-Bird facility. However, there are some functionality tests that can aid in pre-deployment. A bright flashlight can validate whether the instrument sees light at all.
On a bench test one should see between 1000-4000 counts normally with the instrument in the white cap standing up on the benchtop. Use a terminal program to see the raw counts, such as Tera Term, and point a flashlight beam near the white cap. Doing so with a functioning unit will cause the counts to go to approximately a couple of thousand in a hair trigger fashion. It should be possible to decrease the counts on a properly functioning instrument by cupping ones hands around the white cap to shield it from light. It should be easy to get a response of a couple of hundred counts total in doing this. In the field if you shine a flashlight beam directly into the optics will see low level ambient light and it is easy to regulate the output in counts at the low end of the range (less than 1000 counts) when it is functioning normally. If your unit is not properly functioning, it will go from 50-ish to a couple of thousand counts and it will be very difficult or impossible to get an output of a couple of hundred counts. While the ranges of the response may differ between PAR models, these tests can be used with other PAR sensors to verify operation.
There are two optional modifications that can be done to your 9p at our facility (during service or as part of your original order) that will allow the 9p CTD to operate in freshwater deployments. The 9p’s pump will not operate in freshwater without these options.
First, the Modem Pump Control, allows you to control the pump directly, bypassing the requirement for it to see a certain conductivity frequency to activate. (On other CTD’s we can change this conductivity value to allow both freshwater and saltwater).
The second option is the freshwater contact pin, an optional pin modification that allows for the detection of fresh water by the 9p.
Cells that have been contaminated with foreign material generally read low of the actual conductivity. Your zero (in air) conductivity reading is generally unaffected.
The conductivity error due to fouling will generally be proportional to the conductivity value. Conductivity is corrected not as an offset but as a ratio (multiplicative) error compared to a reference.
Salinity is a derivative measurement of temperature, conductivity, and pressure, and should be corrected by adjusting the component measurements. Generally speaking, an error in the conductivity measurement will correlate to a directly proportional error in the salinity measurement.
The temperature and salinity correction for the SUNA can be traced to the experiment outlined in Sakamoto et al. 2009, which is the T/S correction our UCI-based SUNA software uses in post-processing only.
Absorption of UV light in seawater is dominated by dissolved nitrate and bromide ions at wavelengths less than 240 nm. To estimate nitrate, it is necessary to remove the absorption due to bromide. The salinity correction addresses the sea salt extinction coefficients due to bromide. In the real ocean, bromide covaries with NaCl, so we can measure (during calibration) the the bromide absorption due to seawater at one salinity and later predict the absorption due to seawater at any salinity.
Artifical seawater surrogates do not necessarily have the correct bromide absorption to be able to validate the the Sakamoto et al. 2009 salinity correction, so the salinity correction may not product accurate results if your data was not collected in natural seawater.
The measurement range and accuracy of the SBE43 are not defined in discrete units (mL/L, mg/L, µMol/L, etc.) Rather, the range and accuracy specification are expressed as a ratio of the calculated oxygen saturation point. This saturation value depends on the temperature and salinity of the water, decreasing in higher temperatures and higher salinity.
The lower limit of detection of dissolved oxygen concentration is going to be constrained by the accuracy specification, which is a ratio of the calculated oxygen saturation (initial accuracy: +/- 2% of saturation). This saturation value varies depending on the temperature and salinity of the water. Common oxygen saturation values in seawater are in the range of 4-7 mL/L. Using this value as an estimate, you can extrapolate that the accuracy of the sensor in many conditions can be as low as +/- 0.1 mL/L. Therefore, the close you get to zero oxygen concentration, the closer the resolution of your measurement will be to the accuracy spec, until you get below 0.1 – 0.2 mL/L and your measured value is smaller than the nominal error margin.
While the theoretical lower limit of the instrument’s measurement range is zero, the measurement becomes less meaningful the closer your dissolved oxygen measurement gets to 2% of the calculated saturation. For example, if you were in an environment where the oxygen saturation was 7 mL/L but the oxygen concentration measured by the SBE43 was 0.28 mL/L, then your accuracy would effectively be +/- 50% of the measurement, making it relatively useless.
Example Data:
Temperature and Conductivity are two of the most important values taken into consideration when our instrument calculates the practical salinity of seawater. When one sees a change in a measured value, such as temperature, that change will affect your salinity reading in a predictable way, assuming all else is equal. For instance, in an environment where temperature has begun to drift downward you will see a resulting drift of salinity towards being saltier.
Proper cleaning procedures, allowing your CTD to equilibrate at the surface before a profile, updating your calibrations yearly, and bio-fouling prevention are some ways that you can ensure that your instrument will provide accurate salinity data.
A vented copper cover over the sensor can provide some protection against bio-fouling. There is a copper anti-foul guard available for standalone SeaFETs that covers the sensing surfaces.nnIf you use a SeapHOx system, the conductivity cell on the SBE 37-SMP comes equipped with TBTO anti-foul devices at the sample intake and exhaust. These devices will provide a further degree of fouling protection for the ISFET sensor in the pumped flow path. For best results, we recommend replacing the TBTO anti-foul devices before each deployment.nnThere are some antifouling systems that are not recommended:nnWe recommend against electro-chlorination systems. Stray currents in the water could damage the ISFET. Also, adding electrical potential could disrupt the feedback loop between the ISFET and the counter electrode, causing unreliable pH measurements. Finally, a electro-chlorination system doesn’t create just chlorine species, it creates any ions possible in seawater with a lower standard potential then the voltage you are applying. This will create a number of ionic species that will affect the pH of the sample, thereby causing your pH measurements to be inaccurate. In general, we would not recommend putting a ISFET pH sensor inline or downstream from a seawater electrolysis system.nnWe also recommend against UV anti-fouling systems with a SeaFET. There is a risk of exposing the chip to UV radiation, which can cause damage.
The temperature and salinity correction for the SUNA can be traced to the experiment outlined in Sakamoto et al. 2009, which is the T/S correction our UCI-based SUNA software uses in post-processing only.nnAbsorption of UV light in seawater is dominated by dissolved nitrate and bromide ions at wavelengths less than 240 nm. To estimate nitrate, it is necessary to remove the absorption due to bromide. The salinity correction addresses the sea salt extinction coefficients due to bromide. In the real ocean, bromide covaries with NaCl, so we can measure (during calibration) the the bromide absorption due to seawater at one salinity and later predict the absorption due to seawater at any salinity.nnArtifical seawater surrogates do not necessarily have the correct bromide absorption to be able to validate the the Sakamoto et al. 2009 salinity correction, so the salinity correction may not product accurate results if your data was not collected in natural seawater.
Yes, provided the SeaFETTM sensing elements remain ice-free, the instrument works across the broad temperature range of 0 to 50 deg C. The original SeaFETTM prototypes developed at MBARI and SCRIPPS were deployed extensively in the Antarctic for several studies. For example times series data, please see Matson et al. 2011.
For SBE 4 conductivity calibrations, Sea-Bird uses natural seawater that has been carefully collected, stored, UV irradiated, and filtered. Artificial seawater is not adequate if calibration errors are to be kept below 0.010 psu.
Note: SBE 4 is the conductivity sensor in the SBE 9plus, 25, and 25plus profiling CTDs.
The primary difference between natural and artificial seawater is the behavior of conductivity versus temperature. The practical salinity scale 1978 equations include a term rt. This term is expanded into a fourth order equation that describes the variation of conductivity versus temperature for a sample of constant salinity. The equation’s coefficients are derived by fitting to natural seawater samples. Artificial seawater does not have the same conductivity versus temperature characteristic, providing incorrect coefficients and causing a slope error in the calibration.
For calibrations of conductivity sensors other than the SBE 4, Sea-Bird uses artificial seawater (NaCl solution). However, we place an SBE 4 conductivity sensor in each bath, providing a standard for reference to the natural seawater calibration. This allows us to correct errors in the coefficients and slope introduced with the artificial seawater calibration.
For calibration of temperature sensors, Sea-Bird uses artificial seawater (NaCl solution).
The difference between downcast and upcast is most likely related to package wake. When the CTD is mounted under a large water sampler, the variation can be on the order of 5 to 8 meters. This is due to the shadowing of the CTD sensors by the water sampler.
One of the reasons that this is not a simple question is that there are several factors to take into consideration regarding the error margin for practical salinity measurements. Salinity itself is a derived measurement from temperature, conductivity, and pressure, so any errors in these sensors can propagate to salinity. For example, our initial accuracy specification for the SBE 3plus temperature sensor and SBE 4 conductivity sensor on an SBE 9plus CTD is approximately equivalent to an initial salinity accuracy of 0.003 PSU (note that conductivity units of mS/cm are roughly equivalent in terms of magnitude to PSU).
However, another issue to consider is that this accuracy is defined for a clean, well-mixed calibration bath. In the ocean, some of the biggest factors that impact salinity accuracy are 1) sensor drift from biofouling or surface oils for conductivity in particular and 2) dynamic errors that can occur on moving platforms, particularly when conditions are rapidly changing, which will be true for all sensors that measure salinity. Sea-Bird provides recommendations, design features such as a pumped flow path, and data processing routines to align and improve data for the salinity calculation to account for thermal transients and hysteresis, and to match sensor response times. Depending on the environment and the steepness of the gradient, and after careful data processing, this may continue to have an impact on salinity on the order of 0.002 PSU or more, for example. For more details, see Application Note 82.
Lastly, note that salinity in PSU is calculated according to the Practical Salinity Scale (PSS-78), which is defined as valid for salinity ranges from 2 – 42 PSU.
The FIRe System measures changes in chlorophyll fluorescence that occur during a short (100 – 400 ?s) but intense (> 20,000 ?mol photons m-2 s-1) flash of light whereas the PAM approach measures the fluorescence induced by a weak modulated light source while using ‘saturating’ pulses of ~3000 – 10,000 ?mol photons m-2 s-1 to modify fluorescence yields.
The FIRe System also fundamentally differs from a PAM in that the FIRe fully reduces the primary electron acceptor, QA, allowing a simultaneous single closure (STF) event of all photosystem II (PSII) reaction centers whereas the PAM technique generates multiple photochemical charge separations (MTF) that fully reduces QA, the secondary acceptor, QB, and plastoquinone (PQ). By lengthening the measuring protocol the FIRe can also yield MTF data.
For a complete discussion on the mechanistic and practical differences between the two techniques see: Suggett, D.J., K. Oxborough, N.R. Baker, H.L. MacIntyre, T.M. Kana, & R.J. Geider. 2003. Fast repetition rate and pulse amplitude modulation chlorophyll a fluorescence measurements for assessment of photosynthesis electron transport in marine phytoplankton. European Journal of Phycology. 38: 371-84.
Sea-Bird Scientific has developed cosine collectors that are specifically designed to optimize performance in the intended media of operation (air or water). So in water irradiance sensors have cosine collectors that provide an excellent response in water but not in air. In air irradiance sensors provide an excellent cosine response in air but not in water.
Sea-Bird Scientific multispectral 500 series radiometers measure light at each fixed wavelength with an interference filter/detector assembly. The analog output of each detector is amplified and digitized. The amplification stage and noise filtering is fine tuned for each wavelength to produce an optimal saturation limit and frame rate. This maximizes the signal to noise ratio while ensuring that each channel does not saturate during normal operations. The frame rate of each radiometer is fixed anywhere between 1 and 24 Hz depending on the customers specific requirements. 4 and 7 channel radiometers can be purchased in several configurations with different field of views. They have a small diameter to reduce self-shading and generate a digital output for stand-alone operations or they can operate as part of a larger 485 network of sensors (SATNet). 500 series sensors are also very low power devices making them excellent sensors for power limited platforms such as buoys, AUV’s and profiler floats.
Sea-Bird Scientific Hyperspectral HOCR radiometers use a Zeiss spectrograph optimally configured and characterized to measure light between 350 and 800 nm (approximately 136 individual channels). With the HOCR series, a variable integration time is used for all channels in the array and upper and lower thresholds are set so that no channel saturates within that array. Thermal dark current changes that occur within the spectrograph are corrected across the full spectrum with the use of a mechanical dark shutter that closes periodically in the radiometer. A separate frame of data is generated for this dark reading. Frame rates are dependent on the integration time of the device so are considered variable. When light levels are high, the integration time and frame rate are also high, so that you are collecting many frames per second. As the light level decreases, the integration time must increase and therefore the frame rate becomes longer. Integration times range from 4 ms to 2 seconds. HOCR sensors also have a small diameter to reduce self-shading and the same telemetry options are offered. Sea-Bird Scientific also offers a low power, non-SATNet version of the HOCR sensor for remote platforms that are power limited.
The acquisition of conductivity/salinity data alongside the SeaFETTM is recommended. The acquisition of temperature data is not necessary as the SeaFETTM performs temperature measurements. Typically, conductivity and temperature measurements are combined in standard sensor packages. One can use an external temperature measurement calibrated to a relevant scale to confirm the accuracy of the SeaFETTM temperature measurement.
The proximity of the two sensors, as well as, the abruptness of spatial gradients in temperature are both important considerations.
The SUNA V2 determines nitrate concentrations from the shape of the UV absorption curve. The least squares curve fitting algorithm uses calibrated extinction coefficients for nitrate and bromide (strong absorbing species in salt water) to calculate the concentration of nitrate from the UV absorption curve. The algorithm also employs a linear baseline correction that accounts for absorption that is not associated with either nitrate or bromide. The linear baseline correction successfully compensates for CDOM absorption in cases where the CDOM absorption is close to linear in the low UV. The composition of CDOM is dependent on the type of drainage area around a particular watershed and is therefore highly variable. As a result, the shape of CDOM absorption curve can vary from region to region. For this reason, the baseline correction does not always successfully compensate for CDOM absorption. In cases where the CDOM absorption curve mimics the shape of the nitrate absorption curve, a positive bias can occur.
The most common approach for correcting a positive bias caused by CDOM absorption is to correlate the continuous in situ nitrate data provided by the SUNA V2 with nitrate concentrations from discrete water quality samples measured in a laboratory. The bias may then be calculated either as an absolute offset or as a factor. In order to provide the most robust correction possible, the discrete sample size should be sufficiently large to allow for comparisons and the relationship between the in situ and discrete concentrations should be highly correlated.
Instrument specific calibrations are more accurate and correspond to the published accuracy specifications.
The accuracy of the class based calibration is estimated to be 2.2 uM +/- 20%.
The SeaFETTM reports pH measurements on the total scale. Values of pH reported on the total scale represent the effective hydrogen ion concentration with contributions from both free hydrogen ions and those which have reacted with sulfate.
Derivation of Kd from a
In what follows we have left off the dependence on wavelength. In addition we have left off effects due to inelastic scattering.
Modeling Kd(z) requires the inclusion of the depth dependence of the shape of the radiance
distribution. This can be accomplished by using Gershun’s equation:
K(z) = a(z) / ? ? (z)
where a(z) is the absorption coefficient and ?(z) is the average cosine of the light field.
Kd(z) differs from K(z) by only a few percent, so that we may set:
Kd(z) ? a(z) / ? ? (z) .
Berwald et al. (1995) have derived a parametric model for the dependence of ??(z) on ?o for a vertical sun in a black sky. We will assume the same depth dependence for an ordinary sky. This is not precise, but the average cosine varies slowly and has a typical range of only about 10%. The model is:
?o= b / c, where b and c are the total scattering and attenuation coefficients, including water.
? = cz, is the optical depth.
??(?) = ?? + (?(0) – ?? ) exp(-Ptt ).
?? = – 1.59 ?o4 + 1.71 ?o3 – 0.467 ?o2 – 0.347 ?o + 1
?(0)= cosine of refracted solar zenith angle
P?(?o) = – 0.166 ?o2 + 0.341 ?o + 0.0305
Berwald et. al. Limnology and Oceanography 1995, vol. 40, no8, pp. 1347-1357 .
To first order, the vertical resolution is set by the vertical profiling speed. The profiling speed is user configurable (which can be changed during the deployment). At typical profiling speeds of 20 cm/sec, the Thetis Profiler provides the required 0.25 m vertical resolution (even with the slowest 1 Hz sensors).
All data on-board the Thetis Profiler is time stamped using the on-board processor clock. This clock provides 10 ms resolution. The on-board clock is synced to the shore side host controller computer during each surface telemetry session, though the user can chose to when to update the on-board clock.
The numeric difference between psu and ppt is small; both indicate ocean salinity. Prior to 1978, oceanographers referred to the physical quantity ppt (kg salt per kg water in parts per thousand). In 1978, the Practical Salinity Scale (PSS-78) was adopted, which yields a practical salinity from equations, smooth expansions of conductivity ratio, which were carefully fit to the real salinity of diluted North Atlantic seawater. The numeric unit from PSS-78 is psu (practical salinity unit). The primary motivation for psu was consistency; it focused on a trace to a primary conductivity standard (K15) and recognition that ocean ion ratios were not identical. Salinometer work was plagued by an inconsistent standard and the ppt equations included ion ratios from different oceans. So, the trade was a consistent standard and equation that works for a single ion mix instead of exact salinity in other ocean basins. G. Siedler and H. Peters highlighted where PSS-78 and EOS-80 formulas deviate from real salinity and density (e.g., Baltic Sea is difficult, but the deep Pacific has EOS-80 deviations of up to 0.02 kg/m3, implying salinity errors of order 0.02 psu).
In June 2009, a new Thermodynamic Equation of State of Seawater, referred to as TEOS-10, was adopted by the Scientific Committee on Oceanic Research and the International Association of Physical Sciences of the Ocean Working Group 127. The new equation incorporates a more accurate representation of salinity known as Absolute Salinity. Application Note 90 discusses this new equation, and Sea-Bird’s implementation in SBE Data Processing.
The modern oceanographic definition of salinity is the Practical Salinity Scale of 1978 (PSS-78). By definition, PSS-78 is valid only in the range of 2 to 42 psu. Sea-Bird uses the PSS-78 algorithm in our software, without regard to those limitations on the valid range.
Unesco technical papers in marine science 62 “Salinity and density of seawater: Tables for high salinities (42 to 50)” provides a method for calculating salinity in the higher range (access this paper via Unesco’s website).
ITS-90 was adopted in 1990 as the temperature scale; IPTS-68 was the previous standard. The differences are related to redefining certain triple points and other melt or freeze cells that are used as the fundamental standards for temperature. Over the oceanographic ranges of temperature, a linear approximation is used to convert:
IPTS-68 = 1.00024 * ITS-90
The difference is small, but at WOCE levels it is significant.
Note: Salinity, density, and sound velocity are still defined in terms of IPTS-68 temperature. Sea-Bird’s software uses IPTS-68 temperature to calculate these derived parameters, regardless of which temperature scale you select for outputting or plotting temperature.
Application Note 42: ITS-90 Temperature Scale provides a more detailed description.
Upon receipt of an instrument, the initial accuracy is the accuracy when comparing to a known standard. Resolution is the smallest amount of change that a sensor can see.
Direct SV probes measure the time (flight time) required for a sound pulse to travel over a fixed length, using a high-speed clock to measure time. The clock starts when the pulse is emitted, and stops when the pulse is received. Theoretically, you only need to know the path length (and frequency of the clock ? an easy matter) to compute SV:
SV = acoustic path length / flight time.
For a typical acoustic path of 0.1 m, a flight time of 67 microseconds is expected for SV = 1492 m/s.
Two problems associated with direct SV probes are:
- The path length is not readily determined by a ruler measurement. The true length includes some depth into the acoustic transducer at which the pulse actually arises and again some depth where it is actually detected. Consider for example an typical instrument with specified accuracy of 0.05 m/s. For a typical water SV of 1500 m/s and a probe acoustic path of 100 mm, achieving this accuracy requires that length be determined to within (0.05/1500) x 100 mm = 0.003 mm (approximately 1/25 the thickness of a sheet of paper). The acoustic transducer would be of order 1 mm thick, so its dimension is much larger (300 times) than the length associated with the specified accuracy.
- Determining the actual flight time is not as simple as counting clock pulses. There are other time delays in determining both the start of the acoustic pulse and the time of its reception. Recalling that the time sound requires to travel 100 mm is approximately 67 microseconds, to measure SV to within 0.05 m, the flight time must be determined to within (0.05/1492) x 67 microseconds = 2.2 nanoseconds. It is exceedingly difficult to measure time to such precision, especially as the time lag associated with the acoustic transducer is much larger than this ? typically of order 1 microsecond (hundreds of times larger than the permitted error).
The fact is that in designing a direct path SV probe, the determination of length by ruler is only good to 5 or 10% (approximately 100 m/s equivalent uncertainty in SV). The actual determination of SV response therefore must be made in a calibration bath (using a CTD as a reference!), which is how all SV probes are calibrated.
Direct SV probes are often marketed on the principle that the measurement is based only on fundamental physical values of length and time. That is true in theory, but the practice is a different story! Direct SV probe manufacturers do not know the length (or the time) — they just fit the probe response to CTD-computed SV. There is a place for direct SV probes. Having been calibrated in water against a CTD, they do a competent job of measuring SV in other liquids. They will go on working in oil, petrol, milk, beer, etc. — liquids in which CTD measurements have no meaning.
Sea-Bird real-time data acquisition (Seasave V7) and data processing (SBE Data Processing) software supports calculation of Chen-Millero, Del Grosso, and Wilson sound velocities. The algorithms, as implemented in our software, are provided in the software documentation, which is available via the software Help files or in an Appendix in the software manuals.
The Hydrographic Society published Special Publication No. 34 in 1993, “A Comparison Between Algorithms for the Speed of Sound in Seawater”, comparing a number of sound velocity algorithms. The report recommends using the Chen-Millero algorithm for water depths less than 1000 meters and the Del Grosso algorithm for water depths greater than 1000 meters, and recommends that the Wilson algorithm should not be used. Access the report via the Hydrographic Society’s website.
SBE Data Processing includes a module called Seacalc III. Seacalc III can calculate density, sound velocity, and a number of other parameters for a given user input of pressure, temperature, and conductivity (or salinity).
Conductivity cells drift primarily as a function of cell fouling. There are several sources of the fouling:
- Biological growth is the primary source of cell fouling. Rinsing the conductivity cell with clean de-ionized water after each cast helps prevent most growth in the cell. If the cell is not rinsed, or standard tap water is used, growth rates can be severe. As the cell fouls, it will drift towards lower salinity values.
- Surface oil slicks also cause cell fouling. Avoid deploying the CTD through obvious slicks. When working in coastal areas, with higher chances of oil fouling, rinse and soak the cell with a 1% Triton X-100 solution (diluted in clean DI water) to help prevent oil fouling.
See Application Note 2D: Instructions for Care and Cleaning of Conductivity Cells for rinsing, cleaning, and storage procedures.
Because of the nature of fouling, the total cell drift may not be linear. It exhibits rapid small shifts (especially if related to oil fouling) on top of a base line drift. It is important to take water samples to document the behavior. Application Note 31: Computing Temperature and Conductivity Slope and Offset Correction Coefficients from Laboratory Calibrations and Salinity Bottle Samples discusses how to correct the data.
The SUNA V2 contains a 256 channel spectrometer that is programmed to integrate for a specific length of time (usually 300 – 500 ms) while sampling to maximize signal. That is, when the SUNA V2 takes a sample, the spectrograph collects UV light for the length of the integration period. In optically dense waters (e.g. high turbidity or CDOM), very little UV light is transmitted through the water and therefore the spectrometer “sees” a much lower signal. The new SUNA V2 is programmed to automatically increase the integration period to compensate for the low light levels. This enables the instrument to collect a strong signal in extreme environmental conditions.
First off, let’s see what a relatively good Raw Data Plot looks like.

The different phases are the pre-flush phase (dark blue), the ambient baseline reading period (red), the sample reagent pump phase (green), the sample read/reaction phase (purple), and finally the post-flush phase (dark blue). During a “spiked run” the full set of phases are repeated twice.
Using this as an example, you want to see a flat pre- and post-pump phase, a stable (flat) ambient read phase, and a pronounced smooth reaction curve. You may see small bumps here and there due to very small bubbles or other effects but this can be negligible.
The most common failure mode is the bubble spike flag, which triggers when air is introduced into the system, most commonly through the sample line but possibly through incorrectly installed cartridges or tubing.

The bubble failure is typically identified by large jumps and spikes randomly in the data, primarily in the pre- and post- pump phase and the ambient read phase. Air bubbles create an unstable base line (red) which will affect the sensor’s accuracy. In extreme examples it can completely overshadow the reaction curve as well or shift the baseline to the point where your reaction creates a negative value. Air bubbles often exacerbate other issues, like weak pumps, clogged filters, or already low phosphate in your sample.
Since bubbles can come from a few different places there are multiple checks you can do to try to stop bubbles from appearing in your data. The most important check is ensuring that your hydrocycle is fully submerged for the entirety of your deployment, as the sample line being exposed to air will introduce bubbles.
You should check that each of your reagent carts are fully installed. Press down on each reagent cart until you can hear them click and be careful about applying too much force to any of the plastic pieces that may crack and allow for leaks or air.
You can also test the pump volumes of each reagent and sample to see if your filters are clogged or if there is another issue causing the sample injection system to fail, like a leak. You do so by using Cyclehost’s Pump controls. You should choose all pumps and run each for 100 pumps. A healthy system will pump 1-1.3 ml of reagent and 2.5-3 ml of sample.
If you have bubbles already and need to recover, the most thorough method is to follow our maintenance and cleaning instructions in the manual, primarily the extended flush. Running the extended flush multiple times should be enough to clear bubbles from your system if no other issues are evident.
If doing so still fails to recover your instrument’s counts please reach out to technical support with a copy of your hydrocycle data and brief timeline of events.
Manufacturing
Seabird does not manufacture seacables for scientific winch systems and does not specify or endorse any specific cable material. The entire cable assembly must meet the following criteria: A single or multi-core armored cable up to 10,000 meters (32,800 feet) long; an inner core resistance of up to 350 ohms.
The pH sensor will be shipped dry but was pre-conditioned in seawater (generally from Pacific Ocean waters near Hawaii). While conditioning and evaluating the pH sensor, only expose it filtered, sterilized natural seawater. Do not use seawater CRMs (Certified Reference Material), synthetic seawater, deionized water, NaCl Solutions, or tap water.
Before pre-deployment testing, you will need to fill the plumbing around the pH sensor with natural seawater. The pH sensor needs time to acclimate to the ionic concentration of region specific waters. Once wet, the time to recondition the sensor so that it will report within its accuracy specification depends on several factors, including the ionic composition of the seawater used and the amount of time the pH sensor was stored dry. This time can range from several hours to up to three days.
When the seawater bridge between Counter Electrode and ISFET is broken for longer than 10 seconds, it will be necessary to re-condition the sensor. The sensor does not require recalibration after being re-conditioned.
To prepare the sensor for deployment, it is recommended that several days prior to deployment, the isolated battery is connected via the float interface and the pH sensor is stored in water that is similar to the deployment site. The sensor should be stored dry to avoid bio-fouling of the ISFET and the battery may be removed during storage. Seawater creates a half cell bridge between the Counter Electrode and ISFET, and power to that circuit is provided by the isolated 9V cell. Without seawater, the battery is unnecessary and may be disconnected.
The nominal control voltage for the relay is 12 VDC. However, between 5 – 30 VDC will work, applied to pin 4 relative to the ground pin 2 on the Deep SUNA V2. The voltage can be applied to the relay any time after external power is applied to the instrument for a recommended 100 milliseconds. Unless the relay is already switched on, there should be a very quiet (but audible) click when the relay connects power to the SUNA V2 electronics, and the instrument should enter its boot up cycle.
The purpose of the relay is to keep external power applied to the SUNA with very low quiescent current draw, so the typical use case involves the SUNA constantly powered. If the application includes the ability to switch power to the SUNA effectively then the relay feature isn’t necessary. Regardless of how power cycling to the SUNA is controlled, there should be a power-off period of at least 30 seconds between power-on cycles to ensure that the capacitors that prevent a hard shutdown are allowed to completely discharge and allow the SUNA to boot up properly during the next power-on cycle.
No. The Navis does not have charge monitoring capabilities. Typically information of that nature takes a coulomb counter chip, but the overhead with managing the data and powering such a chip is not a current Navis capability and is not expected to be added in the future.
The JT4 bulkhead connector has two options a three pin connector and a four pin connector. If JT4 is a three pin connector, this indicates a standard connector configuration. If JT4 is a four pin connector, that means that the 9plus is configured for 9600 or 19200 serial data and has the uplink feature equipped. Keep in mind that the 11 deck unit must also match the SBE9plus configuration for the serial uplink feature, otherwise it will not communicate properly with the SBE9plus.
There are several considerations when determining whether the deck box and CTD underwater unit will be compatible.
(1) In most cases (with the exception being (2), below), instruments with the “-plus” designation are compatible with each other, but the “-plus” variants are not compatible with the variants that do not have “-plus” in their model number (i.e., an SBE9plus CTD must be used with an SBE11plus, and cannot be used with an older SBE11 deck unit).
(2) If you have an SBE9/11plus system with the serial uplink feature installed, then both the deck box and the CTD must have the same hardware configuration from the factory (either enabled or disabled). Otherwise, no telemetry will be received from the CTD by the deck box.
(3) For older instruments that do not have “-plus” in their model number, you need a matching pair of SBE9 and SBE11. There was no standard configuration, and different CTDs and deck units could have telemetry word/rate differences (4/24, 8/24, 12/24, etc.) and power differences (standard low power or high power). You would need to consult the original documentation that shipped with the instruments or send them to Sea-bird service for a repair evaluation to determine compatibility.
We pressure test each Sea-Bird instrument to the smaller of:
- The housing depth rating, or
- (if pressure sensor installed) The maximum rating of the pressure sensor
Note: Sea-Bird does not pressure test auxiliary sensors supplied by Third Party Manufacturers that are to be integrated with Sea-Bird instruments.
Your entire system is assembled and tested prior to leaving our facility, with software configured to your specific setup. All Sea-Bird manufactured instruments/sensors are calibrated in-house. Sensors from third party manufacturers are calibrated by their manufacturers prior to integration with the CTD system.
There are a number of classes of products that are excluded from the EU requirement for CE certification; underwater sensors and equipment are among the types of products that do not require CE certification. However, Sea-Bird decided to obtain CE certification to ease concerns of customers in the EU.
In 2009 Sea-Bird obtained CE certification for almost all of our instruments; we have CE labels on these instruments and provide the required documentation. There is a CE label on the manual front cover for each certified instrument; see our Model List page to download the manual for a specific instrument to check for the CE label.
Sea-Bird instruments do not have ISO certification. ISO certification does not certify that a manufacturer is producing a high quality product; it merely certifies that a company has a quality control plan that complies with the quality control models adopted by the ISO organization. This does not mean that other quality control systems are inferior. Sea-Bird has intentionally not become ISO-certified, because the ISO quality control model interferes with our own and would make it much harder, slower, and more expensive to remain at the leading edge of oceanographic instrument technology and serve the best interests of ocean scientists.
A zinc anode attracts corrosion and prevents aluminum from corroding until all the zinc is eaten up. Sea-Bird uses zinc anodes on an instrument if it has an aluminum housing and/or end cap. Instruments with titanium or plastic housings and end caps (for example, SBE 37 MicroCAT) do not require an anode.
Check the anode(s) periodically to verify that it is securely fastened and has not been eaten away.
Ordering
Though the naming conventions may seem confusing at first glance, the following key should make your C-star configuration and purchasing process much easier!
The letters following the serial number designate the depth rating of the transmissometer and the wavelength of the LED.
Designator key:
P: Plastic housing rated to 600 meters
D: Deep (Aluminium) housing rated to 6000 meters
R: Red LED, wavelength 657nm
G: Green LED, wavelength 532nm
B: Blue LED, wavelength 470nm
Serial number examples:
CST-1236PR – Plastic unit, 600 meter rated, red 657nm
CST-1219DG – Deep unit, 6000 meter rated, green 532nm
When using the SBE45 thermosalinograph (TSG) with an SBE38 remote temperature sensor, you must use an interface box, as the SBE45 has no direct input for the SBE38. The SBE21 TSG, on the other hand, does have a direct input for the SBE38 remote temperature sensor. Check with your sales or support team contacts if you need help identifying your instruments.
The pH sensor will be shipped dry but was pre-conditioned in seawater (generally from Pacific Ocean waters near Hawaii). While conditioning and evaluating the pH sensor, only expose it filtered, sterilized natural seawater. Do not use seawater CRMs (Certified Reference Material), synthetic seawater, deionized water, NaCl Solutions, or tap water.
Before pre-deployment testing, you will need to fill the plumbing around the pH sensor with natural seawater. The pH sensor needs time to acclimate to the ionic concentration of region specific waters. Once wet, the time to recondition the sensor so that it will report within its accuracy specification depends on several factors, including the ionic composition of the seawater used and the amount of time the pH sensor was stored dry. This time can range from several hours to up to three days.
When the seawater bridge between Counter Electrode and ISFET is broken for longer than 10 seconds, it will be necessary to re-condition the sensor. The sensor does not require recalibration after being re-conditioned.
To prepare the sensor for deployment, it is recommended that several days prior to deployment, the isolated battery is connected via the float interface and the pH sensor is stored in water that is similar to the deployment site. The sensor should be stored dry to avoid bio-fouling of the ISFET and the battery may be removed during storage. Seawater creates a half cell bridge between the Counter Electrode and ISFET, and power to that circuit is provided by the isolated 9V cell. Without seawater, the battery is unnecessary and may be disconnected.
The SeaFET and SeapHOx systems are designed to sample at a fixed depth. If you want to run discreet samples at depth intervals, you will need to find a way to move the system to a specific depth before each sample interval and stop the descent / ascent for the entire pumping and sampling cycle to get a valid CTD / pH / Oxygen sample.
If you are able to communicate with the system through the serial I/O during profiling, you can send a sampling command to the sensor at each depth point and allow it to complete its sample cycle. Consult the manual for each model for the length of time required to complete each sample. Once the sensor provides a sample, you can then move it to the next depth point and repeat.
If you aren’t running real-time communications to the SeaFET/SeapHOx, you could also set it to autonomously sample at a time interval that gives you enough time to move the package to a new depth point between sample cycles. The challenges with this approach would be to know exactly when the sensor is sampling without any direct feedback from the instrument.
The nominal control voltage for the relay is 12 VDC. However, between 5 – 30 VDC will work, applied to pin 4 relative to the ground pin 2 on the Deep SUNA V2. The voltage can be applied to the relay any time after external power is applied to the instrument for a recommended 100 milliseconds. Unless the relay is already switched on, there should be a very quiet (but audible) click when the relay connects power to the SUNA V2 electronics, and the instrument should enter its boot up cycle.
The purpose of the relay is to keep external power applied to the SUNA with very low quiescent current draw, so the typical use case involves the SUNA constantly powered. If the application includes the ability to switch power to the SUNA effectively then the relay feature isn’t necessary. Regardless of how power cycling to the SUNA is controlled, there should be a power-off period of at least 30 seconds between power-on cycles to ensure that the capacitors that prevent a hard shutdown are allowed to completely discharge and allow the SUNA to boot up properly during the next power-on cycle.
SUNAs ordered with the 5mm path length coupler as a factory option will perform much better in low light transmission waters due to the shorter length the light needs to travel leading to less absorption. Equipping your SUNA with the factory bio-wiper option will also perform better and be less susceptible biofouling or buildup of other material that can reduce light transmission.
There are also some maintenance practices and device settings that can give SUNA a better probability of being able to capture enough light for a sample. Enable adaptive integration will trigger the SUNA to increase the lamp on time when light received by the spectrometer is low. It is also important to clean the windows as frequently as possible and monitor lens for scratches. Finally, you want your maximum light spectral counts at the peak wavelength (around 240nm) to be between 45,000 and 55,000 counts in pure or deionized water. This can be viewed in the “Spectra” tab in UCI when sampling or replaying data. If your peak spectrometer output is below 45,000 counts after cleaning the window, you may increase the integration period by 25 to 50 ms if needed (but not more; further changes require a factory recalibration). After adjusting the integration period, always perform a reference spectrum update per the instructions in the SUNA manual.
There are several considerations when determining whether the deck box and CTD underwater unit will be compatible.
(1) In most cases (with the exception being (2), below), instruments with the “-plus” designation are compatible with each other, but the “-plus” variants are not compatible with the variants that do not have “-plus” in their model number (i.e., an SBE9plus CTD must be used with an SBE11plus, and cannot be used with an older SBE11 deck unit).
(2) If you have an SBE9/11plus system with the serial uplink feature installed, then both the deck box and the CTD must have the same hardware configuration from the factory (either enabled or disabled). Otherwise, no telemetry will be received from the CTD by the deck box.
(3) For older instruments that do not have “-plus” in their model number, you need a matching pair of SBE9 and SBE11. There was no standard configuration, and different CTDs and deck units could have telemetry word/rate differences (4/24, 8/24, 12/24, etc.) and power differences (standard low power or high power). You would need to consult the original documentation that shipped with the instruments or send them to Sea-bird service for a repair evaluation to determine compatibility.
On the product page for each instrument, there are two tabs that provide ordering information:
- Click the Configuration tab to see all the features and options available on our price list. The Configuration tab provides explanatory information, illustrations, and photographs describing each item.
- Click the Accessories tab to see cables, mount kits, and/or spare parts for the products.
Third Party Sensor Configuration lists instruments and integration options for sensors produced by other manufacturers (altimeters, fluorometers, transmissometers, etc.).
Most customers purchase spare conductivity and temperature sensors. These sensors are exposed to ocean conditions and therefore more likely to be broken than an internal sensor. It is also very easy to change them because they are independent sensors that plug into the CTD main housing.
Most customers do not purchase spare pressure sensors for the following reasons:
- The pressure sensor is inside the CTD main housing. It is very well protected against damage of any kind, and reliability of this sensor is extremely good.
- The sensor is expensive.
- It is difficult to change the sensor in the field.
IAPSO standard seawater is available in 250 ml vials. For more information and purchase inquiry, e-mail osil@oceanscientific.co.uk.
Sea-Bird does not publish prices on the website. Please contact us for pricing:
- Email seabird@seabird.com,
- Phone +1 425-643-9866, or
- Fill out our Quote Request Form
Sea-Bird makes four main profiling CTD instruments, as well as several profiling CTD instruments for specialized applications.
In order of decreasing cost, the four main profiling CTD instruments are the SBE 911plus CTD, SBE 25plus Sealogger CTD, SBE 19plus SeaCAT Profiler CTD, and SBE 49 FastCAT CTD Sensor:
- The SBE 911plus is the world’s most accurate CTD. Used by most leading oceanographic institutions, the SBE 911plus is recognized for superior performance, reliability, and ease-of-use. Features include: modular conductivity and temperature sensors, Digiquartz pressure sensor, TC-Ducted Flow and pump-controlled time response, 24 Hz sampling, 8 A/D channels and power for auxiliary sensors, modem channel for real-time water sampler control without data interruption, and optional 9600 baud serial data uplink. The SBE 911plus system consists of: SBE 9plus Underwater Unit and SBE 11plus Deck Unit. The SBE 9plus can be used in self-contained mode when integrated with the optional SBE 17plus V2 Searam. The Searam provides battery power, internal 24 Hz data logging, and an auto-fire interface to an SBE 32 Carousel Water Sampler to trigger bottle closures at pre-programmed depths.
- The SBE 25plus Sealogger is the choice for research work from smaller vessel not equipped for real-time operation, or use by multi-discipline scientific groups requiring configuration flexibility and good accuracy and resolution on a smaller budget. The SBE 25plus is a battery-powered, internally-recording CTD featuring the same modular C & T sensors used on the SBE 9plus CTD, an integral strain gauge pressure sensor, 16 Hz sampling, 2 GB of memory, TC-Ducted Flow and pump-controlled time response, and 8 A/D channels plus 2 RS-232 channels and power for auxiliary sensors. Real-time data can be transmitted via RS-232 simultaneous with data recording. The SBE 25plus integrates easily with an SBE 32 Carousel Water Sampler or SBE 55 ECO Water Sampler for real-time or autonomous operation.
- The SBE 19plus V2 SeaCAT Profiler is known throughout the world for good performance, reliability, and ease-of-use. An economical, battery-powered, internally-recording mini-CTD, the SBE 19plus V2 is a good choice for basic hydrography, fisheries research, environmental monitoring, and sound velocity profiling. Features include 4 Hz sampling, 6 differential A/D channels plus 1 RS-232 channel and power for auxiliary sensors, 64 MB of memory, and pump-controlled conductivity time response. Real-time data can be transmitted via RS-232 simultaneous with data recording, The SBE 19plus V2 integrates easily with an SBE 32 Carousel Water Sampler or SBE 55 ECO Water Sampler for real-time or autonomous operation.
- The SBE 49 FastCAT is an integrated CTD sensor intended for towed vehicle, ROV, AUV, or other autonomous profiling applications. Real-time data ? in raw format or in engineering units ? is logged or telemetered by the vehicle to which it is mounted. The SBE 49’s pump-controlled, TC-ducted flow minimizes salinity spiking, and its 16 Hz sampling provides very high spatial resolution of oceanographic structures and gradients. The SBE 49 has no memory or internal batteries. The SBE 49 integrates easily with an SBE 32 Carousel Water Sampler or SBE 55 ECO Water Sampler for real-time operation.
The specialized profiling CTD instruments are the SBE 52-MP Moored Profiler, Glider Payload CTD, and SBE 41/41CP Argo CTD module:
- The SBE 52-MP Moored Profiler is a conductivity, temperature, pressure sensor, designed for moored profiling applications in which the instrument makes vertical profile measurements from a device that travels vertically beneath a buoy, or from a buoyant sub-surface sensor package that is winched up and down from a bottom-mounted platform. The 52-MP’s pump-controlled, TC-ducted flow minimizes salinity spiking. The 52-MP can optionally be configured with an SBE 43F dissolved oxygen sensor.
- The Glider Payload CTD measures conductivity, temperature, and pressure, and optionally, dissolved oxygen (with the modular SBE 43F DO sensor). It is a modular, low-power profiling instrument for autonomous gliders with the high accuracy necessary for research, inter-comparison with moored observatory sensors, updating circulation models, and leveraging data collection opportunities from operational vehicle missions. The pressure-proof module allows glider users to exchange CTDs (and DO sensors) in the field without opening the glider pressure hull.
- Argo floats are neutrally buoyant at depth, where they are carried by currents until periodically increasing their displacement and slowing rising to the surface. The SBE 41/41CP CTD Module obtains the latest CTD profile each time the Argo float surfaces. At the surface, the float transmits in-situ measurements and drift track data to the ARGOS satellite system. The SBE 41/41CP can be integrated with Sea-Bird’s Navis float or floats from other manufacturers. The SBE 41N CTD is integrated with Sea-Bird’s Navis Float with Integrated Biogeochemical Sensors and Navis BGCi + pH Float with Integrated Biogeochemical Sensors.
See Product Selection Guide for a table summarizing the features of our profiling CTDs.
Sea-Bird currently manufactures only 1 moored CTD that can accept auxiliary sensors, the SBE 16plus V2 SeaCAT (and its inductive modem version, the 16plus-IM V2). These instruments measure conductivity and temperature; a pressure sensor is optional. They have 6 differential A/D channels and 1 RS-232 channel available for auxiliary sensors, which can be plugged into the CTD end cap.
The SBE 37 MicroCAT family includes CTDs that are integrated with a dissolved oxygen sensor at the factory.
Notes:
- The SBE 19plus V2 SeaCAT, intended primarily for profiling applications, can also be used in moored mode. The 19plus V2 also has 6 differential A/D channels and 1 RS-232 channel available for auxiliary sensors. When in moored mode, it functions similar to a 16plus V2 with optional pressure sensor.
- The older versions of these products, the SBE 16 / 16plus / 16plus-IM and SBE 19 / 19plus, also accept auxiliary sensors.
See Product Selection Guide for a table summarizing the features of all our moored instruments.
While the highest range does give you the most flexibility in using the CTD, it is at the expense of accuracy and resolution. It is advantageous to use the lowest range pressure sensor compatible with your intended maximum operating depth, because accuracy and resolution are proportional to the pressure sensor’s full scale range. For example, the SBE 9plus pressure sensor has initial accuracy of 0.015% of full scale, and resolution of 0.001% of full scale. Comparing a 2000 psia (1400 meter) and 6000 psia (4200 meter) pressure sensor:
- 1400 meter pressure sensor ? initial accuracy is 0.21 meters and resolution is 0.014 meters
- 4200 meter pressure sensor ? initial accuracy is 0.63 meters and resolution is 0.042 meters
This depends on your own expertise and resources. We have extensive experience in integrating and supporting a wide range of auxiliary sensors, but not everything under the sun. We have a large list of commonly used sensors that we routinely offer for sale (see Third Party Sensor Configuration).
When you purchase any of these auxiliary sensors from Sea-Bird, we are able to apply this experience to integrating the sensors with the CTD. The integration includes installing the sensors (with appropriate mounting kits and cables) in a manner that puts each sensor in the best possible orientation for optimum performance. It also includes configuring the CTD system and software to accept the sensors’ inputs and properly display the data, and testing the entire system, typically in a chilled saltwater bath overnight, to confirm proper operation. Having done the integration, we also support the entire system in terms of follow-on service and end-user support with operational and data analysis questions *. There is significant added value in our integration service, and there is some extra cost for this, compared to doing it yourself. However, we do not base our business on selling services, and the prices charged for Third Party sensors carry minimal mark-ups that vary depending on the pricing we are offered by the manufacturers. In some cases we can sell at the manufacturer’s list price, and in others we have to add margin.
*Notes:
1. As described in our Warranty, auxiliary sensors manufactured by other companies are warranted only to the limit of the warranties provided by their original manufacturers (typically 1 year).
2. Read below for information on repairing / recalibrating auxiliary sensors manufactured by other companies:
Sea-Bird does not repair or recalibrate other manufacturers’ instruments that have been integrated with Sea-Bird equipment. If an auxiliary sensor needs to be repaired or recalibrated, we recommend that you send it directly to the manufacturer. If you send it to Sea-Bird, we will have to send it to the manufacturer, resulting in additional shipping (and possibly customs) expenses for you.
Note: Apparent malfunctioning of an auxiliary sensor can be caused by many things, including incorrect configuration (.con or .xmlcon) file, incorrect instrument setup, incorrect or leaky cables, poor mounting scheme, etc.
-
If you are not certain that the auxiliary sensor needs to be repaired, Sea-Bird can help you troubleshoot the system by phone or e-mail at no charge.
-
Alternatively, if you ship us the entire system, we can troubleshoot at the factory for our standard charges (see the FAQ above this for troubleshooting description). If we determine that the auxiliary sensor does need to be repaired, we will coordinate with you on shipment of the sensor to the manufacturer.
Service
High humidity is often signs of a leak- the SUNA V2 is sealed at the factory and is not meant to be opened outside of service, and an internal desiccant should prevent any moisture left over after assembly from affecting the electronics. In the case that your self test generated by UCI reports back a humidity higher than 30%, or a steady upwards trend over the course of your deployment.
As to the effects of high humidity, it is likely to cause:
– condensation to form on the inner surface of the optics window, under certain ambient conditions. This dramatically impacts the optics and will prevent you from collecting reasonable data.
– corrosion on internal connections and electronics boards, stressing the lamp function and spectrometer. Intense corrosion will lead to equipment failure.
It is difficult to know the time-frame under which the humidity conditions will affect the instrument, so, we recommend getting the SUNA serviced as soon as the humidity reaches about 30%. If you notice any concerning trends, reach out to the support team for recommendations.
The back-scattering measurements are a portion of the total beam attenuation coefficient of the water being sampled. The beam attenuation is measured during the back-scattering calibration. Therefore, the range specification on the data sheet for the BB sensor (0 – 3 or 0 – 5 m^-1) refers to the beam attenuation coefficient range of the calibration.
There is a note on the data sheet that further explains the backscattering specification:
*Backscattering specifications are given in beam cp (m^-1) based on the regression of the response of the instrument relative to the beam cp measured at the coincident wavelength using an ac-s spectrophotometer. Scale factors for backscattering incorporate the target weighting function and the solid angle subtended.
The pH sensor will be shipped dry but was pre-conditioned in seawater (generally from Pacific Ocean waters near Hawaii). While conditioning and evaluating the pH sensor, only expose it filtered, sterilized natural seawater. Do not use seawater CRMs (Certified Reference Material), synthetic seawater, deionized water, NaCl Solutions, or tap water.
Before pre-deployment testing, you will need to fill the plumbing around the pH sensor with natural seawater. The pH sensor needs time to acclimate to the ionic concentration of region specific waters. Once wet, the time to recondition the sensor so that it will report within its accuracy specification depends on several factors, including the ionic composition of the seawater used and the amount of time the pH sensor was stored dry. This time can range from several hours to up to three days.
When the seawater bridge between Counter Electrode and ISFET is broken for longer than 10 seconds, it will be necessary to re-condition the sensor. The sensor does not require recalibration after being re-conditioned.
To prepare the sensor for deployment, it is recommended that several days prior to deployment, the isolated battery is connected via the float interface and the pH sensor is stored in water that is similar to the deployment site. The sensor should be stored dry to avoid bio-fouling of the ISFET and the battery may be removed during storage. Seawater creates a half cell bridge between the Counter Electrode and ISFET, and power to that circuit is provided by the isolated 9V cell. Without seawater, the battery is unnecessary and may be disconnected.
Cells that have been contaminated with foreign material generally read low of the actual conductivity. Your zero (in air) conductivity reading is generally unaffected.
The conductivity error due to fouling will generally be proportional to the conductivity value. Conductivity is corrected not as an offset but as a ratio (multiplicative) error compared to a reference.
Salinity is a derivative measurement of temperature, conductivity, and pressure, and should be corrected by adjusting the component measurements. Generally speaking, an error in the conductivity measurement will correlate to a directly proportional error in the salinity measurement.
The primary maintenance procedures that are outlined in the manual are for the bio-wiper (shutter) installation, the internal battery replacement and the bulkhead connector inspection. The shutter replacement is not always necessary; however, having the copper shutter and face plate parts available to swap out as needed is a good idea.
Otherwise, the optics face should be inspected for film/streaks. The wiper may not work effectively if the copper faceplate condition deteriorates and damages the rubber blade. Some environmental conditions can start to “pit” the face plate surface, shredding the wiper blade. Replacing the face plate should be done if the wiper blade is getting damaged by being dragged across it. Otherwise, cleaning the active optics sensor area usually only requires DI water and a lab wipe (i.e. Kimwipe). Superficial scrapes and scratches on the optics face are unlikely to significantly affect the measurement.
Working with the shutter, moving it for inspection and/or removing it to install a new one, requires the instrument to be powered ON… keeping power to the shutter motor and commanding the open/close positions via software command/control. When moving/removing the shutter, it should NOT BE MOVED MANUALLY! There are gears in the ECO shutter motor that can strip easily with the wrong manual motion, unpowered. The manual motion in the wrong direction and speed, can overcome some of the gear ratios at play when they are back-driven.
Terminal emulator programs (as opposed to ECO View) are the most direct platform for working with the ECO’s. However, their use depends on one’s preference for how to interface with the instruments.
An RTC (real time clock) is an electronic component which maintains an accurate time reference for the CTD. In the past, clock chips could be periodically calibrated to account for slow drift. As of the early 2000s, Sea-bird has been using components with improved stability to the point where recalibration is no longer necessary over the lifespan of an instrument.
SUNAs ordered with the 5mm path length coupler as a factory option will perform much better in low light transmission waters due to the shorter length the light needs to travel leading to less absorption. Equipping your SUNA with the factory bio-wiper option will also perform better and be less susceptible biofouling or buildup of other material that can reduce light transmission.
There are also some maintenance practices and device settings that can give SUNA a better probability of being able to capture enough light for a sample. Enable adaptive integration will trigger the SUNA to increase the lamp on time when light received by the spectrometer is low. It is also important to clean the windows as frequently as possible and monitor lens for scratches. Finally, you want your maximum light spectral counts at the peak wavelength (around 240nm) to be between 45,000 and 55,000 counts in pure or deionized water. This can be viewed in the “Spectra” tab in UCI when sampling or replaying data. If your peak spectrometer output is below 45,000 counts after cleaning the window, you may increase the integration period by 25 to 50 ms if needed (but not more; further changes require a factory recalibration). After adjusting the integration period, always perform a reference spectrum update per the instructions in the SUNA manual.
There are several considerations when determining whether the deck box and CTD underwater unit will be compatible.
(1) In most cases (with the exception being (2), below), instruments with the “-plus” designation are compatible with each other, but the “-plus” variants are not compatible with the variants that do not have “-plus” in their model number (i.e., an SBE9plus CTD must be used with an SBE11plus, and cannot be used with an older SBE11 deck unit).
(2) If you have an SBE9/11plus system with the serial uplink feature installed, then both the deck box and the CTD must have the same hardware configuration from the factory (either enabled or disabled). Otherwise, no telemetry will be received from the CTD by the deck box.
(3) For older instruments that do not have “-plus” in their model number, you need a matching pair of SBE9 and SBE11. There was no standard configuration, and different CTDs and deck units could have telemetry word/rate differences (4/24, 8/24, 12/24, etc.) and power differences (standard low power or high power). You would need to consult the original documentation that shipped with the instruments or send them to Sea-bird service for a repair evaluation to determine compatibility.
When your max lamp counts drop below 30,000 during the self test and cannot recover with cleaning, you can send the lamp in for inspection.
If your lamp time remaining is less than 25% then it is best to send the SUNA in for a lamp replacement. We will automatically replace lamps during service if they have less than 30% time remaining, as we want the SUNA to have enough lamp hours to last until your next yearly service.
When your max lamp counts drop below 30,000 during the self test and cannot recover with cleaning, you can send the lamp in for inspection.
If your lamp time remaining is less than 25% then it is best to send the SUNA in for a lamp replacement. We will automatically replace lamps during service if they have less than 30% time remaining, as we want the SUNA to have enough lamp hours to last until your next yearly service.
Brush-cleaning and replatinizing should be performed at Sea-Bird. We cannot extend warranty coverage if you perform this work yourself.
The brush-cleaning and replatinizing process requires specialized equipment and chemicals, and the disassembly of the sensor. If performed incorrectly, you can damage the cell. Additionally, the sensor must be re-calibrated when the work is complete.
Sea-Bird determines whether brush-cleaning and replatinizing is required based upon how far the calibration has drifted from the original calibration. Typically, a conductivity sensor on a profiling CTD requires brush-cleaning and replatinizing every 5 years.
The post-cruise calibration contains important information for drift calculations. The post-cruise calibration is performed on the cell as we received it from you, and is an indicator of how much the sensor has drifted in the field. Information from the post-cruise calibration can be used to adjust your data, based on the sensor’s drift over time. See Application Note 31: Computing Temperature and Conductivity Slope and Offset Correction Coefficients from Laboratory Calibrations and Salinity Bottle Samples.
If the sensor has drifted significantly (based on the data from the post-cruise calibration), Sea-Bird performs a C & P to restore the cell to a state similar to the original calibration. After the C & P, the sensor is calibrated again. This calibration serves as the starting point for future data, and for the sensor’s next drift calculation.
The C & P tends to return the cell to its original state. However, there are many subtle factors that may result in the post-C & P calibration not exactly matching the original calibration. Basically, the old platinizing is stripped off and new platinizing is plated on. Anything in this process that alters the cell slightly will result in a difference from the original calibration. We compare the calibration after C & P with the original calibration, not to make any drift analysis, but to make sure we did not drastically alter the cell, or that the cell was not damaged during the C & P process.
Configuration Sheets detail instrument communication settings, system configuration (auxiliary sensors, which channels are set up for which sensors), and sensor calibration coefficients. Configuration sheets are provided with the instrument, in both paper form (may be part of the manual) and on the CD-ROM.
Configuration Sheet locations vary, depending on the type of instrument and when it was shipped. If you cannot locate them, contact Sea-Bird and we will email copies.
It is our policy to update firmware in instruments while they are here for calibration at no cost to the customer, but it is not our policy to routinely upgrade circuit cards. On some very old units that are being upgraded to support more external sensors, new pressure sensors, or other repairs, we sometimes discount the new circuit cards as part of the larger upgrade, as that makes the work easier for us to complete.
For calibration of the temperature and conductivity sensors, only the sensor modules need to be sent to Sea-Bird. It is not necessary to send the CTD main housing. See Shipping SBE 9plus, 25, and 25plus Temperature and Conductivity Sensors for details.
It is usually not necessary to recalibrate the pressure sensor as frequently as the temperature and conductivity sensors. Experience has shown that the sensor’s sensitivity function almost never changes; only the offset drifts. The offset drift can easily be measured by reading deck pressure against a barometer. This small drift is easily corrected (Seasave V7 and SBE Data Processing provide an entry for the offset drift in the instrument .con or .xmlcon file).
- SBE 9plus and 25plus — If the pressure sensor does need to be calibrated, the entire CTD must be shipped to Sea-Bird.
- SBE 25 — If the pressure sensor does need to be calibrated, only the modular SBE 29 pressure sensor needs to be sent to Sea-Bird. It is not necessary to send the CTD main housing.
Sea-Bird opened a calibration/service center in Kempten, Germany in 2011, providing duty-free servicing for EU customers. The dedicated technical support staff and calibration technicians were extensively trained by Sea-Bird experts. Calibration cross-referencing between the US and Germany facilities ensures Sea-Bird factory quality and accuracy. The German facility stocks a full range of parts and supplies to support repairs. Details.
The Anti-Foulant Device is an expendable device that is installed on each end of the conductivity cell, so that any water that enters the cell is treated. Anti-Foulant Devices are typically used with moored instruments (SBE 16, 16plus, 16plus-IM, 16plus V2, 16plus-IM V2, 37-SM, 37-SMP, 37-SMP-IDO, 37-SMP-ODO, 37-SI, 37-SIP, 37-SIP-IDO, 37-IM, 37-IMP, 37-IMP-IDO, 37-IMP-ODO, HydroCAT, HydroCAT-EP), thermosalinographs (SBE 21 and 45), glider CTDs (Glider Payload CTD), moored profilers (SBE 52-MP), and drifters (SBE 41/41CP Argo float CTDs), and optionally with SBE 19plus, 19plus V2, and 49 profilers.
Anti-Foulant Devices have no effect on the calibration, because they do not affect the geometry of the conductivity cell in any way. The Anti-Foulant Devices are mounted at either end of the conductivity cell. For an in-depth explanation of how Sea-Bird makes the conductivity measurement, see Conductivity Sensors for Moored and Autonomous Operation.
Useful deployment life varies, depending on several factors. We recommend that customers consider more frequent anti-foulant replacement when high biological activity and strong current flow (greater dilution of the anti-foulant concentration) are present. Moored instruments in high growth and strong dilution environments have been known to obtain a few months of quality data, while drifters that operate in non-photic, less turbid deep ocean environments may achieve years of quality data. Experience may be the strongest determining factor in specific deployment environments. Sea-Bird recommends that you keep track of how long the devices have been deployed, to allow you to purchase and replace the devices when needed.
Note that the anti-foulant device does not actually dissolve, so there is no way to visually determine if the anti-foulant device is still effective.
The cost of the anti-foulant devices is small compared to the deployment costs, so we recommend that you replace the devices before each deployment. This will provide the maximum bio-fouling protection, resulting in long-term data quality.
Shelf Life and Storage: The best way to store Anti-Foulant Devices is in an air-tight, opaque container. The rate of release of anti-foulant is based on saturation of the environment. The anti-foulant will release until the environment is fully saturated (100% saturated) and then it will no longer release any anti-foulant. So if you keep Anti-Foulant Devices sealed well in an air-tight container, theoretically they will stay good for extended periods of time. Exposure to direct sunlight can also affect the release of anti-foulant; we recommend storage in an opaque container.
Handling:
- For details, refer to the Material Safety Data Sheet, enclosed with the shipment and available on our MSDS page.
- Anti-Foulant Devices are not classified by the U.S. DOT or the IATA as hazardous material.
For SBE 4 conductivity calibrations, Sea-Bird uses natural seawater that has been carefully collected, stored, UV irradiated, and filtered. Artificial seawater is not adequate if calibration errors are to be kept below 0.010 psu.
Note: SBE 4 is the conductivity sensor in the SBE 9plus, 25, and 25plus profiling CTDs.
The primary difference between natural and artificial seawater is the behavior of conductivity versus temperature. The practical salinity scale 1978 equations include a term rt. This term is expanded into a fourth order equation that describes the variation of conductivity versus temperature for a sample of constant salinity. The equation’s coefficients are derived by fitting to natural seawater samples. Artificial seawater does not have the same conductivity versus temperature characteristic, providing incorrect coefficients and causing a slope error in the calibration.
For calibrations of conductivity sensors other than the SBE 4, Sea-Bird uses artificial seawater (NaCl solution). However, we place an SBE 4 conductivity sensor in each bath, providing a standard for reference to the natural seawater calibration. This allows us to correct errors in the coefficients and slope introduced with the artificial seawater calibration.
For calibration of temperature sensors, Sea-Bird uses artificial seawater (NaCl solution).
For Sea-Bird instruments that use alkaline D-cells, Sea-Bird uses Duracell MN 1300, LR20. While rare, we have seen a few problems with cheaper batteries over the years: they are more likely to leak, may vary in size (leading to loose batteries causing a bad power connection), and may not last as long.
Adhesive Teflon tape (actually, UHMW tape — Ultra High Molecular Weight polyethylene) provides insulation to prevent damage due to contact of dissimilar metals. It is typically used by Sea-Bird on the inside of hose clamps used for mounting instruments, where U-bolts hold a Carousel Water Sampler frame to an extension stand, etc. The tape can be ordered from Sea-Bird; part number 30409 is 1 inch wide x 0.1 inch thick x 1 foot long (2.5 cm x 0.25 cm x 0.3 m). It can also be purchased from the manufacturer, Crown Plastics (see www.crownplastics.com for local distributors).
Plug the ends of the conductivity cell to prevent the cleaning solution from getting into the cell. Then soak the entire instrument in white vinegar for a few minutes. After scraping off the barnacles and marine growth, rinse the instrument well with fresh water.
We do not advise using hydrochloric acid (HCl) to clean instrument housings. Such highly corrosive acids will not hurt the anodized surfaces, but will attack any bare aluminum — including the aluminum in the cracks — and can also damage O-rings, connectors, and other sensor components.
Note: If sending the instrument to Sea-Bird for calibration, remove as much biological material as possible before shipping. Sea-Bird cannot place an instrument with a large amount of biological material on the housing in our calibration bath; if we need to clean the exterior before calibration, we will charge you for this service.
For minimizing future growth on the housing, completely wrap the instrument housing with plastic tape. The bio-organisms still grow, but after recovery it is easy to peel off the tape, shells and mussels and all!
The housings of some of our instrument are made from anodized aluminum. In our experience it is very common to see color change when anodized housings are moored in seawater. We even see some discoloration during the brief time instruments undergo calibration and testing.
There may be several causes of discoloration:
- Zinc from the protective anodes tends to deposit on the surface, causing the color to lighten toward gray.
- Some seawater components, for example, carbonates, may precipitate onto the surfaces.
- The anodized coating does not completely cover the aluminum: at microscopic scale the coating has the appearance of a dry lake bed ? there are patches of anodizing surrounded by cracks. These cracks allow water to reach bare aluminum and cause local oxidation that is light in color. Fortunately, once a thin oxide coating forms on aluminum, further corrosion tends to be inhibited. Unless you see severe pitting, there is usually no danger to the safety of the housing.
No, Sea-Bird does not perform low or narrow range calibrations on our CTDs. However, CTDs are used successfully in many freshwater environments.
Conductivity calibrations performed at Sea-Bird are valid in the range of 0 – 9 S/m (or 0 – 7 S/m, as specified for some instruments), and the calibration coefficients can be applied in freshwater for accurate calculations of conductivity.
Sea-Bird recognizes that calibration using natural seawater and IAPSO standards for ocean conductivity ranges may result in a small offset and possible slope errors near zero conductivity. For example, the estimated magnitude of offset error is < 0.002 S/m, and of slope error is < 0.002 S/m per 1 S/m change. This is an example of a conservative error estimate for initial accuracy of conductivity sensors used in freshwater, which can be challenging to calculate due to lack of a freshwater standard. However, sensor precision will be near the resolution (0.00004 S/m). Sea-Bird CTDs provide high precision and sensor stability, allowing an accurate measure of conductivity gradients (dC/dz) or water sample differences, regardless of ‘true’ conductivity values. For these reasons, Sea-Bird CTDs that have been calibrated in seawater can be used successfully in many freshwater systems.
Lastly, note that the Practical Salinity Scale (PSS-78) is defined as valid for salinity ranges from 2 – 42 PSU. For additional references on freshwater algorithms used in the limnology field, see the following literature:
- Millero, Frank J. 2000. Equation of State for Freshwater. Aquatic Geochemistry, 6: 1 – 17.
- Pawlowicz, R. 2008. Calculating the Conductivity of Natural Waters. L&O: Methods 6, 489 – 501.
An ISUS should run at approximately 1Hz. Check the amount of storage space left on the internal memory; old data files should be downloaded or deleted from the disk on a regular basis. Additionally, the Messages.log files should be periodically removed. Download and/or delete these files to restore normal operation.
The stability of the SeaFETTM Ocean pH sensor is expected to be 0.005 pH units on the timescale of weeks to months (Martz et al. 2010). At minimum, the SeaFETTM should be calibrated yearly. The body of data collected by the community of SeaFETTM users generally suggests that the stability of the ISFET-based pH measurement offers an improvement by orders of magnitude when compared to glass electrode based pH sensors.
Wherever possible the SeaFETTM should be deployed in association with a water sampling program in order to collect water for spectrophotometric pH determination or another external measurement technique. Additionally, coincident measurement of multiple carbonate system parameters, allow the stability of the SeaFETTM to be assessed. These approaches have been carried out by a number of researchers over the past several years.
Shipping: Sea-Bird carefully packs the CTD in foam for shipping. If you are shipping the CTD or conductivity sensor, carefully pack the instrument using the original crate and packing materials, or suitable substitutes.
Use: Cracks at the C-Duct end of the conductivity cell are most often caused by:
- Hitting the bottom, which can cause the T-C Duct to flex, resulting in cracking at the end of the cell.
- Removing the soaker tube from the T-C duct in a rough manner, which also causes the T-C Duct to flex. Pulling the soaker tube off at an angle can be especially damaging over time to the cell. Pull the soaker tube off straight down and gently.
- Improper disassembly of the T-C ducted temperature and conductivity sensors (SBE 25, 25plus, and 9plus) when removing them for shipment to Sea-Bird for calibration. See Shipping SBE 9plus, 25, and 25plus Temperature and Conductivity Sensors for the correct procedure.
Note: If a Tygon tube attached to the conductivity cell has dried out, yellowed, or become difficult to remove, slice (with a razor knife or blade) and peel the tube off of the conductivity cell rather than twisting or pulling the tube off.
General recommendations:
- Profiling CTD — recalibrate once/year, but possibly less often if used only occasionally. We recommend that you return the CTD to Sea-Bird for recalibration. (In principle, it is possible for calibration to be performed elsewhere, if the calibration facility has the appropriate equipment andtraining. However, the necessary equipment is quite expensive to buy and maintain.) In between laboratory calibrations, take field salinity samples to document conductivity cell drift.
- Moored CTD — recalibrate at least once/year, but possibly more often depending on the degree of bio-fouling in the water.
- Thermosalinograph — recalibrate at least once/year, but possibly more often depending on the degree of bio-fouling in the water.
- DO sensor —
— SBE 43 — recalibrate once/year, but possibly less often if used only occasionally and stored correctly (see Application Note 64), and also depending on the amount of fouling and your ability to do some simple validations (see Application Note 64-2)
— SBE 63 — recalibrate once/year, but possibly less often if used only occasionally and stored correctly and also depending on the amount of fouling and your ability to do some simple validations (see SBE 63 manual) - pH sensor —
— SBE 18 pH sensor or SBE 27 pH/ORP sensor — recalibrate at the start of every cruise, and then at least once/month, depending on use and storage
— Satlantic SeaFET pH sensor — recalibrate at least once/year. See SeaFET page for details (How often does the SeaFET need to be calibrated?). - Transmissometer — usually do not require recalibration for several years. Recalibration at the manufacturer’s factory is the most practical method.
Profiling CTDs:
We often have requests from customers to have some way to know if the CTD is out of calibration. The general character of sensor drift in Sea-Bird conductivity, temperature, and pressure measurements is well known and predictable. However, it is very difficult to know precisely how far a CTD calibration has drifted over time unless you have access to a very sophisticated calibration lab. In our experience, an annual calibration schedule will usually maintain the CTD accuracy to within 0.01 psu in Salinity.
Conductivity drifts as a change in slope as a result of accumulated fouling that coats the inside of the conductivity cell, reducing the area of the cell and causing an under-reporting of conductivity. Fouling consists of both biological growth and accumulated oils and inorganic material (sediment). Approximately 95% of fouling occurs as the cell passes through oil and other contaminants floating on the sea surface. Most conductivity fouling is episodic, as opposed to gradual and steady drift. Most fouling events are small and mostly transitory, but they have a cumulative affect over time. A severe fouling event, such as deployment through an oil spill, could have a dramatic but only partially recoverable effect, causing an immediate jump shift toward lower salinity. As fouling becomes more severe, the fit becomes increasingly non-linear and offsets and slopes no longer produce adequate correction, and return to Sea-Bird for factory calibration is required. Frequently checking conductivity drift is likely to be the most productive data assurance measure you can take. Comparing conductivity from profile to profile (as a routine check) will allow you to detect sudden changes that may indicate a fouling event and the need for cleaning and/or re-calibration.
Temperature generally drifts slowly, at a steady rate and predictably as a simple offset at the rate of about 1-2 millidegrees per year. This is approximately equal to 1-2 parts per million in Salinity error (very small).
Pressure sensor drift is also an offset, and annual comparisons to an accurate barometer to determine offset will generally keep the sensor within specification for several years, particularly as the sensors age over time.
Typically, Sea-Bird can calibrate the instrument and perform minor repairs within 3 – 4 weeks, plus shipping time. However, this may vary, depending on current backlog. Before shipping an instrument to us, go to our Online RMA and Service Request Form page to obtain an RMA number, so that we know your instrument is on the way and can schedule appropriately. If time is critical, contact us before shipping to verify that we can meet your schedule.
Notes:
- The typical 3 – 4 week turnaround does not apply to recalibrating / repairing auxiliary sensors produced by other manufacturers. Recalibration / repair of these sensors must be performed by the manufacturers.
- Sea-Bird opened a calibration and repair center in Germany in 2011, which can provide faster shipping for European customers.
The answer to this question depends on your budget and your level of confidence that the entire system is functioning properly. When Sea-Bird receives CTDs that have integrated auxiliary sensors produced by other manufacturers, we test the functionality of the entire system. For a standard charge, we:
- Visually inspect the physical condition of the auxiliary sensor, connector, and interface cable.
- Visually inspect the mounting scheme of the auxiliary sensor on the CTD (a poor mounting scheme can result in poor data).*
- (For voltage sensors) Measure the open voltage and block voltage to ensure that the auxiliary sensor responds through the full 0 – 5V range.
- Check that the auxiliary sensor reads correctly when submerged in our cold salt water test baths for 30 – 60 minutes.
If the auxiliary sensor does not meet our standards*, we recommend that the sensor be sent to the other manufacturer for service. If the sensor is sent to the other manufacturer, we perform the same tests when it returns to us after servicing. Additionally, we update the configuration (.con or .xmlcon) file with any new calibration coefficients.
*Note: Sea-Bird can fix mounting scheme issues; we do not send the sensor to the other manufacturer for this.
Sea-Bird does not repair or recalibrate other manufacturers’ instruments that have been integrated with Sea-Bird equipment. If an auxiliary sensor needs to be repaired or recalibrated, we recommend that you send it directly to the manufacturer. If you send it to Sea-Bird, we will have to send it to the manufacturer, resulting in additional shipping (and possibly customs) expenses for you.
Note: Apparent malfunctioning of an auxiliary sensor can be caused by many things, including incorrect configuration (.con or .xmlcon) file, incorrect instrument setup, incorrect or leaky cables, poor mounting scheme, etc.
- If you are not certain that the auxiliary sensor needs to be repaired, Sea-Bird can help you troubleshoot the system by phone or e-mail at no charge.
- Alternatively, if you ship us the entire system, we can troubleshoot at the factory for our standard charges (see the FAQ above this for troubleshooting description). If we determine that the auxiliary sensor does need to be repaired, we will coordinate with you on shipment of the sensor to the manufacturer.
Alkaline batteries can be shipped installed in the instrument. See Shipping Batteries for information on shipping instruments with Lithium or Nickel-Metal Hydride (NiMH) batteries.
Field Procedures & Deployment
The SUNA V2 has capacitors that maintain internal power for to the electronics long enough for a proper shutdown process when external power is removed. However, these capacitors must completely discharge between power cycles, or else the SUNA may fail to properly boot up when external power is reapplied. If your SUNA is stuck in a state where it will not respond to external power, unplug the bulkhead connector completely from the SUNA and wait 30-60 seconds before reapplying external power again.
The polled mode setting allows the user to program the SUNA to sample when a command is sent. Customers who would like to integrate an SDI-12 controller with their SUNA should use the polled mode setting. Please note that the SDI-12 operation is not available on SUNA V2 Deep sensors.
Unfortunately, users cannot currently program their SUNA to start at a preferred time. As soon as the SUNA is powered, the instrument will begin it’s programmed sampling mode on the hour. Users can use the offset feature to change the start time. For example, an offset value of 300 (5 min) changes the start time by five minutes, for example, from 06:00 to 06:05.
The continuous mode setting allows the user to program their SUNA to run continuously for an indefinite amount of time. When power is supplied to the SUNA, it will start data acquisition without an end time or maximum number of frames to measure. In general, we do not recommend this mode for long periods of time because the lamp of the SUNA can burn out. As a general rule of thumb, the SUNA lamp should be replaced when it reaches 750 hours.
The periodic mode setting allows the user to select how often, and how long sample intervals are based on frame-based or time-based operation.
For example, if a user would like to program their SUNA to sample every two hours, they would use a sample interval of two hours.
The user would then select either frame-based or time-based operation
For frame-based operation, the user selects the number of light frames the SUNA will sample for.
For time-based operation the user selects how many seconds of light frames the SUNA will sample for.
When the SUNA is powered, the instrument will begin it’s programmed sampling mode on the hour. Users can use the offset feature to change the start time. For example, an offset value of 300 (5 min) changes the start time by five minutes, for example, from 06:00 p.m. to 06:05 p.m.
High humidity is often signs of a leak- the SUNA V2 is sealed at the factory and is not meant to be opened outside of service, and an internal desiccant should prevent any moisture left over after assembly from affecting the electronics. In the case that your self test generated by UCI reports back a humidity higher than 30%, or a steady upwards trend over the course of your deployment.
As to the effects of high humidity, it is likely to cause:
– condensation to form on the inner surface of the optics window, under certain ambient conditions. This dramatically impacts the optics and will prevent you from collecting reasonable data.
– corrosion on internal connections and electronics boards, stressing the lamp function and spectrometer. Intense corrosion will lead to equipment failure.
It is difficult to know the time-frame under which the humidity conditions will affect the instrument, so, we recommend getting the SUNA serviced as soon as the humidity reaches about 30%. If you notice any concerning trends, reach out to the support team for recommendations.
The SBE9/11+ system does not have the capability to support any instrumentation data or signals via its sea cable that are not directly connected to the SBE9+ CTD and associated carousels.
There is a hardware upgrade on the 9/11+ system that provides a serial RS-232 data uplink. This is a relatively constrained feature on the 9/11+ system, that allows a serial RS-232 data stream to be passed up the sea cable and saved as a separate data file.
NOTE: This upgrade is installed in the 9/11+ at the factory and operates at 9600 baud, requiring
that the 9/11+ be configured/operating at this same baud rate.
None of this is compatible with a video signal to be integrated into this system. Additional hardware components inline with the sea cable that are not supplied by Sea-Bird Scientific would be required. This custom application is not currently supported.
The lifespan of the probe is typically between 3 months and 2 years, depending on where and how often it is deployed, storage conditions, and the particular electrode performance. It is a good idea to periodically check the storage solution to make sure that it is still full, and you can use Parafilm on the bottle cap and store the sensor vertically for best results. Routine checks on performance can help prevent premature sensor drift.
Some indications that we use to evaluate if the electrode needs replacement:
– Physical condition – Sometimes the probe will crystalize and you can see large gaps (air pockets) in the reference electrode, whereas a good probe will be more uniform.
– Slow response time – Another symptom that a probe is going bad. For example, if it takes more than 10-15 minutes to reach a stable pH value, or it might not stabilize at all.
– Poor readings, such as high pH residuals or big changes in raw voltage output. For example, if it reads < 1.7 VDC in pH 4 solution. We look at all of the indications above to make the best determination about whether an electrode needs to be replaced. Generally, the best way to evaluate your pH probe is to calibrate your sensor frequently (such as once a month) using consistent and fresh buffer solutions, and track the change in response time, raw voltage output and pH residuals over time.
Temperature and Conductivity are two of the most important values taken into consideration when our instrument calculates the practical salinity of seawater. When one sees a change in a measured value, such as temperature, that change will affect your salinity reading in a predictable way, assuming all else is equal. For instance, in an environment where temperature has begun to drift downward you will see a resulting drift of salinity towards being saltier.
Proper cleaning procedures, allowing your CTD to equilibrate at the surface before a profile, updating your calibrations yearly, and bio-fouling prevention are some ways that you can ensure that your instrument will provide accurate salinity data.
For a more comprehensive look at our salinity calculations please refer to App Note 14, which is hosted on our website.
In general, the best practice is to store instruments at temperatures above freezing (0 degrees C), and below 35 degrees C (keeping out of direct sunlight while on deck whenever possible).
It is best to minimize exposure at high temperatures, as this could contribute to instrument drift.
At low temperatures, below freezing, the conductivity cell is susceptible to cracking, so it is recommended to store the instrument dry. Note, if the CTD has auxiliary sensors installed, storage recommendations can be found in the appropriate manual for individual sensors. Some instruments must be stored in a liquid solution or in filtered seawater, but this will be made evident in the documentation provided to you upon purchase. It is crucial that these sensors are protected from cold temperatures that may cause these liquids to freeze.
Replacement batteries for the 37 Microcat family are available from multiple retailers online, as Seabird Scientific recommends that Saft AA LS14500 3.6V lithium cells be used as the primary batteries. If this brand is not available in your area please reach out to sales or support for assistance.
Seabird does not manufacture seacables for scientific winch systems and does not specify or endorse any specific cable material. The entire cable assembly must meet the following criteria: A single or multi-core armored cable up to 10,000 meters (32,800 feet) long; an inner core resistance of up to 350 ohms.
The recommended nominal flow rate is 1 liter/second (15.8 gallons/minute).
The pH sensor will be shipped dry but was pre-conditioned in seawater (generally from Pacific Ocean waters near Hawaii). While conditioning and evaluating the pH sensor, only expose it filtered, sterilized natural seawater. Do not use seawater CRMs (Certified Reference Material), synthetic seawater, deionized water, NaCl Solutions, or tap water.
Before pre-deployment testing, you will need to fill the plumbing around the pH sensor with natural seawater. The pH sensor needs time to acclimate to the ionic concentration of region specific waters. Once wet, the time to recondition the sensor so that it will report within its accuracy specification depends on several factors, including the ionic composition of the seawater used and the amount of time the pH sensor was stored dry. This time can range from several hours to up to three days.
When the seawater bridge between Counter Electrode and ISFET is broken for longer than 10 seconds, it will be necessary to re-condition the sensor. The sensor does not require recalibration after being re-conditioned.
To prepare the sensor for deployment, it is recommended that several days prior to deployment, the isolated battery is connected via the float interface and the pH sensor is stored in water that is similar to the deployment site. The sensor should be stored dry to avoid bio-fouling of the ISFET and the battery may be removed during storage. Seawater creates a half cell bridge between the Counter Electrode and ISFET, and power to that circuit is provided by the isolated 9V cell. Without seawater, the battery is unnecessary and may be disconnected.
Cells that have been contaminated with foreign material generally read low of the actual conductivity. Your zero (in air) conductivity reading is generally unaffected.
The conductivity error due to fouling will generally be proportional to the conductivity value. Conductivity is corrected not as an offset but as a ratio (multiplicative) error compared to a reference.
Salinity is a derivative measurement of temperature, conductivity, and pressure, and should be corrected by adjusting the component measurements. Generally speaking, an error in the conductivity measurement will correlate to a directly proportional error in the salinity measurement.
The primary maintenance procedures that are outlined in the manual are for the bio-wiper (shutter) installation, the internal battery replacement and the bulkhead connector inspection. The shutter replacement is not always necessary; however, having the copper shutter and face plate parts available to swap out as needed is a good idea.
Otherwise, the optics face should be inspected for film/streaks. The wiper may not work effectively if the copper faceplate condition deteriorates and damages the rubber blade. Some environmental conditions can start to “pit” the face plate surface, shredding the wiper blade. Replacing the face plate should be done if the wiper blade is getting damaged by being dragged across it. Otherwise, cleaning the active optics sensor area usually only requires DI water and a lab wipe (i.e. Kimwipe). Superficial scrapes and scratches on the optics face are unlikely to significantly affect the measurement.
Working with the shutter, moving it for inspection and/or removing it to install a new one, requires the instrument to be powered ON… keeping power to the shutter motor and commanding the open/close positions via software command/control. When moving/removing the shutter, it should NOT BE MOVED MANUALLY! There are gears in the ECO shutter motor that can strip easily with the wrong manual motion, unpowered. The manual motion in the wrong direction and speed, can overcome some of the gear ratios at play when they are back-driven.
Terminal emulator programs (as opposed to ECO View) are the most direct platform for working with the ECO’s. However, their use depends on one’s preference for how to interface with the instruments.
The SeaFET and SeapHOx systems are designed to sample at a fixed depth. If you want to run discreet samples at depth intervals, you will need to find a way to move the system to a specific depth before each sample interval and stop the descent / ascent for the entire pumping and sampling cycle to get a valid CTD / pH / Oxygen sample.
If you are able to communicate with the system through the serial I/O during profiling, you can send a sampling command to the sensor at each depth point and allow it to complete its sample cycle. Consult the manual for each model for the length of time required to complete each sample. Once the sensor provides a sample, you can then move it to the next depth point and repeat.
If you aren’t running real-time communications to the SeaFET/SeapHOx, you could also set it to autonomously sample at a time interval that gives you enough time to move the package to a new depth point between sample cycles. The challenges with this approach would be to know exactly when the sensor is sampling without any direct feedback from the instrument.
The nominal control voltage for the relay is 12 VDC. However, between 5 – 30 VDC will work, applied to pin 4 relative to the ground pin 2 on the Deep SUNA V2. The voltage can be applied to the relay any time after external power is applied to the instrument for a recommended 100 milliseconds. Unless the relay is already switched on, there should be a very quiet (but audible) click when the relay connects power to the SUNA V2 electronics, and the instrument should enter its boot up cycle.
The purpose of the relay is to keep external power applied to the SUNA with very low quiescent current draw, so the typical use case involves the SUNA constantly powered. If the application includes the ability to switch power to the SUNA effectively then the relay feature isn’t necessary. Regardless of how power cycling to the SUNA is controlled, there should be a power-off period of at least 30 seconds between power-on cycles to ensure that the capacitors that prevent a hard shutdown are allowed to completely discharge and allow the SUNA to boot up properly during the next power-on cycle.
SUNAs ordered with the 5mm path length coupler as a factory option will perform much better in low light transmission waters due to the shorter length the light needs to travel leading to less absorption. Equipping your SUNA with the factory bio-wiper option will also perform better and be less susceptible biofouling or buildup of other material that can reduce light transmission.
There are also some maintenance practices and device settings that can give SUNA a better probability of being able to capture enough light for a sample. Enable adaptive integration will trigger the SUNA to increase the lamp on time when light received by the spectrometer is low. It is also important to clean the windows as frequently as possible and monitor lens for scratches. Finally, you want your maximum light spectral counts at the peak wavelength (around 240nm) to be between 45,000 and 55,000 counts in pure or deionized water. This can be viewed in the “Spectra” tab in UCI when sampling or replaying data. If your peak spectrometer output is below 45,000 counts after cleaning the window, you may increase the integration period by 25 to 50 ms if needed (but not more; further changes require a factory recalibration). After adjusting the integration period, always perform a reference spectrum update per the instructions in the SUNA manual.
There are two ways the Navis float can start a mission without the user explicitly starting pressure activation or mission execute:
(1) Not freezing the float:
If the float is not frozen (I F command) before the communications dongle is removed, the float controller will eventually timeout.
(2) Communications dongle noise:
If the user sends the I F command, then disconnects and the communications dongle, there can be small electrical pulses as the connection is removed that may cause the float to wake back up. The float will then timeout and start a mission. This can be prevented by adding a break switch in-line with the Navis communications dongle that can be turned off before physically disconnecting it from the float.
Both of these events are intentionally implemented as a failsafe in case a user accidentally deployed a float before activating the mission.
No. The Navis does not have charge monitoring capabilities. Typically information of that nature takes a coulomb counter chip, but the overhead with managing the data and powering such a chip is not a current Navis capability and is not expected to be added in the future.
There are several considerations when determining whether the deck box and CTD underwater unit will be compatible.
(1) In most cases (with the exception being (2), below), instruments with the “-plus” designation are compatible with each other, but the “-plus” variants are not compatible with the variants that do not have “-plus” in their model number (i.e., an SBE9plus CTD must be used with an SBE11plus, and cannot be used with an older SBE11 deck unit).
(2) If you have an SBE9/11plus system with the serial uplink feature installed, then both the deck box and the CTD must have the same hardware configuration from the factory (either enabled or disabled). Otherwise, no telemetry will be received from the CTD by the deck box.
(3) For older instruments that do not have “-plus” in their model number, you need a matching pair of SBE9 and SBE11. There was no standard configuration, and different CTDs and deck units could have telemetry word/rate differences (4/24, 8/24, 12/24, etc.) and power differences (standard low power or high power). You would need to consult the original documentation that shipped with the instruments or send them to Sea-bird service for a repair evaluation to determine compatibility.
We do not specify a maximum line resistance. However, the Inductive Modem systems are very tolerant of the resistivity of seawater. It is typically only a consideration when the system is being deployed in freshwater lakes, etc. where the salinity level is a lot lower.
We recommended using one of the two oceanographic cables below or those of equivalent specification:
1. Loos & Co. 3×19 Galvanized Oceanographic Cable, Plastic Impregnated
2. WireCo WorldGroup Macwhyte 3×19 Space-Lay Plastic Impregnated and Coated Wire Rope
The most important aspect is the resilience of the cable jacket. Any cuts, tears, or breaks in the insulation will create a shorter path to the seawater ground which will result in the the level of the signal on the lower side of the cable being attenuated.
Lithium battery packs are not suitable for use with 16plus units that have the 5T or 5M pumps installed as the drain on the battery is significantly higher. This effect causes deployments to be shorter and is not reflected in the SBE Deployment Endurance software, making planning your deployment more difficult.
There are two optional modifications that can be done to your 9p at our facility (during service or as part of your original order) that will allow the 9p CTD to operate in freshwater deployments. The 9p’s pump will not operate in freshwater without these options.
First, the Modem Pump Control, allows you to control the pump directly, bypassing the requirement for it to see a certain conductivity frequency to activate. (On other CTD’s we can change this conductivity value to allow both freshwater and saltwater).
The second option is the freshwater contact pin, an optional pin modification that allows for the detection of fresh water by the 9p.
SUNAs ordered with the 5mm path length coupler as a factory option will perform much better in low light transmission waters due to the shorter length the light needs to travel leading to less absorption. Equipping your SUNA with the factory bio-wiper option will also perform better and be less susceptible biofouling or buildup of other material that can reduce light transmission.
There are also some maintenance practices and device settings that can give SUNA a better probability of being able to capture enough light for a sample. Enable adaptive integration will trigger the SUNA to increase the lamp on time when light received by the spectrometer is low. It is also important to clean the windows as frequently as possible and monitor lens for scratches. Finally, you want your maximum light spectral counts at the peak wavelength (around 240nm) to be between 45,000 and 55,000 counts in pure or deionized water. This can be viewed in the “Spectra” tab in UCI when sampling or replaying data. If your peak spectrometer output is below 45,000 counts after cleaning the window, you may increase the integration period by 25 to 50 ms if needed (but not more; further changes require a factory recalibration). After adjusting the integration period, always perform a reference spectrum update per the instructions in the SUNA manual.
The ECO-PAR, due to the nature of PAR sensors, cannot be accurately calibrated outside of the Sea-Bird facility. However, there are some functionality tests that can aid in pre-deployment. A bright flashlight can validate whether the instrument sees light at all.
On a bench test one should see between 1000-4000 counts normally with the instrument in the white cap standing up on the benchtop. Use a terminal program to see the raw counts, such as Tera Term, and point a flashlight beam near the white cap. Doing so with a functioning unit will cause the counts to go to approximately a couple of thousand in a hair trigger fashion. It should be possible to decrease the counts on a properly functioning instrument by cupping ones hands around the white cap to shield it from light. It should be easy to get a response of a couple of hundred counts total in doing this. In the field if you shine a flashlight beam directly into the optics will see low level ambient light and it is easy to regulate the output in counts at the low end of the range (less than 1000 counts) when it is functioning normally. If your unit is not properly functioning, it will go from 50-ish to a couple of thousand counts and it will be very difficult or impossible to get an output of a couple of hundred counts. While the ranges of the response may differ between PAR models, these tests can be used with other PAR sensors to verify operation.
There are two optional modifications that can be done to your 9p at our facility (during service or as part of your original order) that will allow the 9p CTD to operate in freshwater deployments. The 9p’s pump will not operate in freshwater without these options.
First, the Modem Pump Control, allows you to control the pump directly, bypassing the requirement for it to see a certain conductivity frequency to activate. (On other CTD’s we can change this conductivity value to allow both freshwater and saltwater).
The second option is the freshwater contact pin, an optional pin modification that allows for the detection of fresh water by the 9p.
Oftentimes one will see data in their cast that looks erroneous or out of spec, but reviewing the timeline of each cast and the events which transpired can explain these jumps. If you are starting your cast while your CTD is on deck then the time during which the unit is running in air can be spiky or erratic, but this should be solved after the unit has been fully submerged and the pump has activated. The pump on time setting controls how fast the system will turn on the pump after deployment, so filtering out your deckside data can be done by calculating the number of scans to exclude using your pump on time setting, samples to average setting, and native sampling rate of your CTD.
Bubbles in the flow line can also cause spikes in your data towards the start of your deployment if the system isn’t able to normalize at the surface. We typically recommend units stay near the surface for 2-5 minutes in order to allow air bubbles to escape.
Finally, for additional resources in troubleshooting and smoothing data outliers for your CTD data, refer to our documentation on Seabird University.
The primary maintenance procedures that are outlined in the manual are for the bio-wiper (shutter) installation, the internal battery replacement and the bulkhead connector inspection. The shutter replacement is not always necessary, but, having the copper shutter and face plate parts available to swap out as needed, is a good idea.
Otherwise, the optics face should be inspected for film/streaks. The wiper may not work effectively if the copper faceplate condition deteriorates and damages the rubber blade. Some environmental conditions can start to “pit” the face plate surface, shredding the wiper blade. Replacing the face plate should be done if the wiper blade is getting damaged by being dragged across it. Otherwise, cleaning the active optics sensor area usually only requires DI water and a lab wipe (i.e. Kimwipe). Superficial scrapes and scratches on the optics face are unlikely to significantly affect the measurement.
Working with the shutter, moving it for inspection and/or removing it to install a new one, requires the instrument to be powered ON… keeping power to the shutter motor and commanding the open/close positions via software command/control. When moving/removing the shutter, it should NOT BE MOVED MANUALLY! There are gears in the ECO shutter motor that can strip easily with the wrong manual motion, unpowered. The manual motion in the wrong direction and speed, can overcome some of the gear ratios at play when they are back-driven.
Terminal emulator programs (as opposed to ECO View) are the most direct platform for working with the ECO’s. However, their use depends on one’s preference for how to interface with the instruments.
There are several considerations when determining whether the deck box and CTD underwater unit will be compatible.nn(1) In most cases (with the exception being (2), below), instruments with the “-plus” designation are compatible with each other, but the “-plus” variants are not compatible with the variants that do not have “-plus” in their model number (i.e., an SBE9plus CTD must be used with an SBE11plus, and cannot be used with an older SBE11 deck unit).nn(2) If you have an SBE9/11plus system with the serial uplink feature installed, then both the deck box and the CTD must have the same hardware configuration from the factory (either enabled or disabled). Otherwise, no telemetry will be received from the CTD by the deck box.nn(3) For older instruments that do not have “-plus” in their model number, you need a matching pair of SBE9 and SBE11. There was no standard configuration, and different CTDs and deck units could have telemetry word/rate differences (4/24, 8/24, 12/24, etc.) and power differences (standard low power or high power). You would need to consult the original documentation that shipped with the instruments or send them to Sea-bird service for a repair evaluation to determine compatibility.
The pH sensor will be shipped dry but was pre-conditioned in seawater (generally from Pacific Ocean waters near Hawaii). While conditioning and evaluating the pH sensor, only expose it filtered, sterilized natural seawater. Do not use seawater CRMs (Certified Reference Material), synthetic seawater, deionized water, NaCl Solutions, or tap water.nnBefore pre-deployment testing, you will need to fill the plumbing around the pH sensor with natural seawater. The pH sensor needs time to acclimate to the ionic concentration of region specific waters. Once wet, the time to recondition the sensor so that it will report within its accuracy specification depends on several factors, including the ionic composition of the seawater used and the amount of time the pH sensor was stored dry. This time can range from several hours to up to three days.nnWhen the seawater bridge between Counter Electrode and ISFET is broken for longer than 10 seconds, it will be necessary to re-condition the sensor. The sensor does not require recalibration after being re-conditioned. nnTo prepare the sensor for deployment, it is recommended that several days prior to deployment, the isolated battery is connected via the float interface and the pH sensor is stored in water that is similar to the deployment site. The sensor should be stored dry to avoid bio-fouling of the ISFET and the battery may be removed during storage. Seawater creates a half cell bridge between the Counter Electrode and ISFET, and power to that circuit is provided by the isolated 9V cell. Without seawater, the battery is unnecessary and may be disconnected.
There are two ways the N2 can start a mission without the user explicitly starting pressure activation or mission execute.nnNot Freezing the float:nIf the float is not frozen (I F command) and the dongle is removed, the N2 will eventually timeout. This is more of a precaution in the case the user forgot to start the mission and deployed the float. nnDongle Noise:nIf the user sends the I F command, then attempts to disconnect and the dongle removal is not clean, this may cause the float to wake back up. The float will then timeout and start a mission. Here it would be recommended that a switch is added inline to the dongle (similar to what we have in production)
The only warning of eventual failure is that prior to full battery depletion, the float will typically see a voltage drop with 5-15% of the float life remaining.
This issue can have a few different causes. The most common cause is noise from your Data I/O connector on your CTD. This noise can be caused by a shorted serial deployment cable or water intrusion under the dummy plug on the I/O connector. nnTo solve this issue, we need to identify what is introducing the noise or causing the bad connection. We first suggest that you check the 6-pin data I/O connector “J3” on the SBE19plusV2 bottom endcap. If you notice it being damp or having any corrosion to the pins, cracked or bent pins, or an improperly fitting seal with the cable, those could all cause these intermittent failures. Next, if there is a Y-cable installed on connector “J3,” perform the same inspection on the 4-pin male connector on the pump/data I/O Y-cable. Again, look for anything out of the ordinary as these are the most common failure points.nnIf these connections seem to be in fine condition, if you have another Y cable available you can attempt to swap this to see if this resolves the issue. If this works, the original Y cable should be discarded and replaced.
Cells that have been contaminated with foreign material generally read low of the actual conductivity. Your zero (in air) conductivity reading is generally unaffected.nnThe conductivity error due to fouling will generally be proportional to the conductivity value. Conductivity is corrected not as an offset but as a ratio (multiplicative) error compared to a reference.nnSalinity is a derivative measurement of temperature, conductivity, and pressure, and should be corrected by adjusting the component measurements. Generally speaking, an error in the conductivity measurement will corellate to a directly proportional error in the salinity measurement.
For convenience while examining differences in density between two water parcels, Sigma-density values are typically used by oceanographers. Sigma-density values allow the oceanographer to focus on the last 6 to 7 digits in the density value (when assuming 5 decimal place resolution), as this is where most of the variation in density occurs. Sigma-density values are also a shorthand way for representing density of a water parcel with some specific modification to one of the density computational inputs, like pressure or temperature.
Examples:
- Sigma = (rho(t,s,p) – 1000) kg/m3
- Sigma-t = (rho(s,t,p=0) – 1000) kg/m3 (density at atmospheric pressure)
- Sigma-theta = (rho(t=theta,s,0) – 1000 kg/m3 (density with effect of adiabatic cooling/heating effect [using potential temperature] and the pressure effect removed).
So, though the true density of water is always a value that is non-negative, when testing instruments on the bench (zero salinity) or in freshwater systems, the computed density can be < 1000 kg/m3. In this situation, when converting density to a Sigma-density value, it is possible for the Sigma-density value to be negative.
Example: S = 0, t = 5 deg C, and pressure = 0
rho(S,t,pressure) = 999.96675 kg/m3
Sigma-t (t,S,0) = – 0.03325
For more information on the Practical Salinity Scale (1978) and the Equation of State for Seawater (EOS-80), refer to UNESCO Technical Papers of Marine Science 44.
Note: Many UNESCO marine science publications are available through UNESCO’s website. Go to http://unesdoc.unesco.org/ulis/ioc/.
- In the Series title box, select UNESCO technical papers in marine science.
- Select Widen the search to all UNESCO documents/publications.
- Click the OK button.
Adhesive Teflon tape (actually, UHMW tape — Ultra High Molecular Weight polyethylene) provides insulation to prevent damage due to contact of dissimilar metals. It is typically used by Sea-Bird on the inside of hose clamps used for mounting instruments, where U-bolts hold a Carousel Water Sampler frame to an extension stand, etc. The tape can be ordered from Sea-Bird; part number 30409 is 1 inch wide x 0.1 inch thick x 1 foot long (2.5 cm x 0.25 cm x 0.3 m). It can also be purchased from the manufacturer, Crown Plastics (see www.crownplastics.com for local distributors).
Plug the ends of the conductivity cell to prevent the cleaning solution from getting into the cell. Then soak the entire instrument in white vinegar for a few minutes. After scraping off the barnacles and marine growth, rinse the instrument well with fresh water.
We do not advise using hydrochloric acid (HCl) to clean instrument housings. Such highly corrosive acids will not hurt the anodized surfaces, but will attack any bare aluminum — including the aluminum in the cracks — and can also damage O-rings, connectors, and other sensor components.
Note: If sending the instrument to Sea-Bird for calibration, remove as much biological material as possible before shipping. Sea-Bird cannot place an instrument with a large amount of biological material on the housing in our calibration bath; if we need to clean the exterior before calibration, we will charge you for this service.
For minimizing future growth on the housing, completely wrap the instrument housing with plastic tape. The bio-organisms still grow, but after recovery it is easy to peel off the tape, shells and mussels and all!
The BOSS was specifically designed for bolt-on integration with an Argo profiling float. As such, the design and telemetry interfaces are not set up for stand alone or real-time profiling.
The free-falling profiler is designed to profile away from a small boat or large ship to avoid any potential shadow effects. The instrument is deployed by hand from the leeward side of the vessel and allowed to descend while the vessel drifts downwind. When the profiler is pulled back up to the surface, the fins cause the instrument to maintain its location and come straight up. Using this method, the optical profiles can be performed at a safe distance from the vessel.
In later SatView Versions, the Pressure Tare button is located under the ancillary view at the “package” level. To open the ancillary view at the package level: Notice the white section of the SatView main window – this is where your loaded instruments appear. Within this white section, at the very top there is a suitcase icon, with the individual instruments treed out underneath. Right click to bring up a drop down menu, select “View List” and “Ancillary View” to open the package level ancillary window that contains the Pressure Tare button.
Wet-pluggable (also referred to as wet-mateable or MCBH) connectors, an option on all of our underwater instruments, may be mated in wet conditions (click here for a photo comparison). Their pins do not need to be dried before mating. By design, water on the connector pins is forced out as the connector is mated. However, they must not be mated or un-mated while submerged. Wet-pluggable connectors have a non-conducting guide pin to assist pin alignment & require less force to mate, making them easier to mate reliably under dark or cold conditions, compared to our Impulse XSG/RMG connectors (XSG/RMG connectors may not seal well in extreme cold; we recommend connecting cables in warm ship’s lab rather than on deck for these conditions). Like XSG/RMG connectors, wet-pluggables need proper lubrication & require care during use to avoid trapping water in sockets.
Wet-pluggable connectors do add additional cost to the instrument. The increase in price is dependent on the number of pins on each connector, and the number of connectors on your instrument. When should you consider configuring your instrument with wet-pluggable connectors? Consider the following guidelines:
- Internal recording with a profiling CTD (for example, SBE 9plus with 17plus V2, SBE 19plus V2, SBE 25plus) — Connecting/disconnecting frequently to the CTD is typical for these systems, for uploading of the internally recorded data. Wet-pluggable connectors are recommended for these applications.
- Autonomous water sampling (SBE 32 Carousel with AFM or 17plus V2, or SBE 55 ECO Water Sampler) and internal recording with a profiling CTD — Connecting/disconnecting to the underwater electronics is required after every cast, to re-arm the electronics for autonomous water sampling. Connecting/disconnecting is often done on deck, where the connectors are exposed to splashing and rain; wet-pluggable connectors are strongly recommended for these applications.
- Real-time data acquisition with a profiling CTD (for example, SBE 9plus with 11plus Deck Unit, SBE 19plus V2 with PDIM and SBE 33 or 36 Deck Unit, SBE 25plus with PDIM and SBE 33 or 36 Deck Unit) — The underwater units in these systems are plugged into the sea cable, and typically are disconnected infrequently. Wet-pluggable connectors are not as important for this application.
- Moored instruments —
— If data upload after recovery will occur on deck to allow for quick redeployment, wet-pluggable connectors are recommended.
— If data upload after recovery will occur in a lab, wet-pluggable connectors are not as important for this application.
Note: Prior to 2005, the wet-pluggable connectors available had a rubber-to-metal seal that could break down with prolonged use (3 – 5 years); seal breakdown will lead to instrument flooding. Sea-Bird recommended frequent inspection of the connectors for damage. We also discouraged the use of wet-pluggable connectors for moored deployments, because they cannot be inspected during a prolonged deployment.
From 2005 to 2007, Sea-Bird transitioned to the WB (water block) type of wet-pluggable connectors. WB connectors have a water block that minimizes the possibility of instrument flooding; we do not discourage the use of these types of connectors for moored deployments. If you have wet-pluggable connectors on your instrument and are unsure of which type you have, contact Sea-Bird.
Application Note 83: Deployment of Moored Instruments contains a checklist, which is intended as a guideline to assist you in developing a checklist specific to your operation and instrument setup.
Mating and Unmating Connectors:
It is important to prepare and mate connectors correctly, both in terms of the costs to repair them and to preserve data quality. Leaking connectors cause noisy data and even potential system shutdowns. Application Note 57: Connector Care and Cable Installation describes the proper care and installation of connectors for Sea-Bird instruments. The Application Note covers connector cleaning and cable or dummy plug installation, locking sleeve installation, and cold weather tips.
Checking for Leakage and Cleaning Corrosion on Connectors:
If there has been leakage, it will show up as green-colored corrosion product. Performing the following steps can usually reverse the effect of the leak:
- Thoroughly clean the connector with water, followed by alcohol.
- Give the connector surfaces a light coating of silicon grease.
Re-mate the connectors properly — see Application Note 57: Connector Care and Cable Installation and 9-minute video covering O-ring, connector, and cable maintenance.
Replacing Connectors:
- The main concern when replacing a bulkhead connector is that the o-rings on the connector and end cap must be prepared and installed correctly; if they are not, the instrument will flood. See the question below for general procedure on handling o-rings.
- Use a thread-locking compound on the connector threads to prevent the new connector from loosening, which could also lead to flooding.
- If the cell guard must be removed to open the instrument, take extra care not to break the glass conductivity cell.
“The requirements of a GPS to enable data collection with Sea-Bird Scientific’s SatView software are:
1. NMEA 0183 Output
2. Serial connection The SAS GPS option includes a prewired Garmin model GPS 17xHVS. This model is designed for marine use, and connects to serial port on your computer. It can be mounted to a pole for the duration of the cruise.
A suitable hand held model, is the GPS 72H from Garmin and has both the NEMA output and a serial connection. A optional serial cable is required, and also a power cable, if running from an external power source is desired.”
Inspecting and Cleaning O-Rings and Mating Surfaces:
- Remove any water from the o-rings and mating surfaces with a lint-free cloth or tissue.
- Visually inspect the o-rings and mating surfaces for dirt, nicks, cuts, scratches, lint, hair, and any signs of corrosion; these could cause the seal to fail. Clean the surfaces, and clean or replace the o-rings as necessary.
- Apply a light, even coat of 100% silicon o-ring lubricant (Parker Super O Lube) to the o-rings and mating surfaces. For an end cap o-ring, a ball of lubricant the size of a pea is about all that is needed. Too much lubricant can cause the seal to fail as much, if not more, than no grease. Do not use petroleum-based lubricant (car grease, Vaseline, etc.), as it will cause premature failure of the rubber.
CAUTION: Parker makes another product, Parker O Lube, that is petroleum-based. Do not use this product; verify that you are using Parker Super O Lube. - After lubricating the o-ring, immediately reassemble the end cap or connector, verifying that no hairs or lint have collected on the lubricated o-ring.
Replacing O-Rings:
- End Cap O-Rings: We recommend scheduled replacement of end cap o-rings approximately every 3 years, to prevent leaks caused by normal o-ring wear.
- Connector O-Rings: Replacing connector o-rings requires de-soldering and re-soldering the connector wires, which makes it a more difficult task. Therefore, we recommend replacement of connector o-rings when needed, not on a routine, scheduled basis.
Additional Information:
- 9-minute video covering O-ring, connector, and cable maintenance.
- Short, silent video of application of lubricant to o-ring.
- Short, silent video of application of lubricant to o-ring mating surface (note the use of a plastic dental syringe— no sharp points to scratch the housing — to apply the lubricant).
Yes, the SeaFET™ pH sensor comes with a flow through cell with fittings that can be plumbed with a pump for flow-through operations. For in situ deployments, we recommend the SBE 5P submersible pump.
General
Large numbers of Sea-Bird conductivity instruments have been used in Arctic and Antarctic programs.
Special accommodation to keep temperature, conductivity, oxygen, and optical sensors at or above 0 C is advised. Often, the CTD is brought inside protective doors between casts to achieve this.
Conductivity Cell
When freezing is possible, we recommend that the conductivity sensor be stored dry. Remove larger droplets of water by blowing through the cell. Do not use compressed air, which typically contains oil vapor. Attach a length of Tygon tubing to each end of the conductivity cell to close the cell ends. See Application Note 2D: Instructions for Care and Cleaning of Conductivity Cells for details.
There are several considerations to weigh when contemplating deployments at low temperatures in general, and in frazil or pancake ice:
- Ensure that the instrument is at or above water temperature before it is deployed. If the cell gets colder than 0 to -2 ºC while on deck, when it enters the water a layer of ice forms inside the cell as the cell warms to ocean temperature. If ice forms inside the conductivity cell, measurements will be low of correct until the ice layer melts and disappears. Thin layers of ice will not hurt the conductivity cell, but repeated ice formation on the electrodes will degrade the conductivity calibration (at levels of 0.001 to 0.020 psu) and thicker layers of ice can lead to glass fracture and permanent damage of the cell.
- For accurate measurements, keep ice out of the sensing region of the conductivity cell. The conductivity measurement involves determining the electrical resistance of the water inside the sensor. Ice is essentially a non-conductor. To the extent that ice displaces the water, the conductivity will register (very) misleadingly low. Some type of screening is necessary to keep ice out of the cell. This is relatively easy to arrange for the Sea-Bird conductivity cell, which is an electrode-type cell, because its sensing region is totally inside a long tube; plastic mesh could be positioned at each end and would have zero effect on accuracy and stability.
The above considerations apply to all known conductivity sensor types, whether electrode or inductive types.
If deploying at low temperatures but no surface frazil or pancake ice is present, rinse the conductivity cell in one of the following salty solutions (salty water depresses the freezing point) to prevent freezing during deployment. But this does not mean you can store the cell in one of these solutions outside . . . it will freeze.
- Solution of 1% Triton in sterile seawater (use 0.5-micron filtered seawater or boiled seawater), or
- Brine solution (distilled seawater or homemade salt solution that is higher than 35 psu in salinity).
Note that there is still a risk of forming ice inside the conductivity cell if deploying through frazil or pancake ice on the surface, if the freezing point of the salt water is the same as the water temperature. Therefore, we recommend that you deploy the conductivity cell in a dry state for these deployments.
Commercially available alcohol or glycol antifreezes contain trace amounts of oils that will coat the conductivity cell and the electrodes, causing a calibration shift, and consequently result in errors in the data. Do not use alcohol or glycol in the conductivity cell.
Temperature Sensor
In general, neither the accuracy of the temperature measurement nor the survival of the temperature sensor will be affected by ice.
Oxygen Sensor
For the SBE 43 and SBE 63 Dissolved Oxygen sensor, avoid prolonged exposure to freezing temperature, including during shipment. Do not store with water (fresh or seawater), Triton solution, alcohol, or glycol in the plenum. The best precaution is to keep the sensor indoors or in some shelter out of the cold weather.
We recommend keeping the connectors on your meter lubricated using a good quality silicone spray lubricant, such as 3M Silicone Spray or Loctite 8021 spray. These can be purchased at your local hardware store. Avoid silicone grease. It is messy and attracts contaminants.
Do not use WD-40. It will destroy connectors.
The most complete backup system would be another SBE 9plus, to allow for very rapid system swaps. This is important if your stations are close together and there is limited time between CTD casts. However, it is the most expensive option.
The next step down would be an SBE 9plus without sensors. In this case, a system failure would require swapping sensors and pumps to the new unit. This is not difficult, but it is somewhat time consuming. If you have several hours between casts it should not be a problem.
The next option would be to carry spare boards and try and troubleshoot the problem and replace boards. If you have a technician that can do this it is not a bad option. However, it requires some clean and dry lab space to open the CTD and work. You will also have to properly re-seal the CTD. Based upon experience, the SBE 9plus does not fail very often. The most common failure is the main DC-to-DC converter. Other than that, there are very few system failures. However, there are several components that can be damaged through mistakes or misuse. The most catastrophic, other that losing the whole CTD, is to plug the sea cable into the bottom contact connector on the bottom end cap; if this happens, several circuit boards will be destroyed (Note: In 2007 Sea-Bird began using a female bulkhead connector on the 9plus for the bottom contact switch, to differentiate from the sea cable connector and prevent this error. If desired, older CTDs can be retrofitted with the female connector.).
If the budget allows it, we recommend getting a complete backup SBE 9plus, including sensors. If there is any problem, return the malfunctioning instrument for repair and continue sampling with the spare instrument. A complete backup also provides you with spare sensors, so you can rotate 1 set through calibration and continue to operate.
The base sensing suite includes a FastCat CTD, a combined fluorescence and turbidity sensor, and a PAR sensor. The current supported list of instruments for Thetis include:
- CTD: SeaBird FastCat CTD (SBE49)
- Dissolved oxygen: SeaBird SBE43 or SBE63
- Chlorophyll: Sea-Bird Scientific ECO or WETStar series
- CDOM: Sea-Bird Scientific ECO or WETStar series
- Turbidity: Sea-Bird Scientific ECO series
- Optical absorption and attenuation: Sea-Bird Scientific ACS
- PAR: ECO PARS (Sea-Bird Scientific)
- Nitrate: Satlantic SUNA V2
- Irradiance and Radiance: Satlantic OCR and HOCR
- 3-axis velocity: NortekUSA Aquadopp
Additional sensors can be accommodated but may require NRE. Sensors requiring flow though (pumped) measurements can be accommodated with our system.
The mounting system used for the instruments facilitates replacing sensors by the user. Adding new instruments may require new brackets.
Yes, vertical is usually preferable. In the presence of consistent currents and suspended sediment, we have seen instances where a horizontal conductivity cell is scoured by the abrasive effect of the flow. When scouring is particularly intense, the electrodes can be stripped of their electroplated platinum-black coating, driving the calibration toward fresher readings. Sedimentation (silting) in the cell also drives the readings fresh of correct.
Mounting the instrument vertically avoids abrasive flow and sediment build-up while allowing wave motions and Bernoulli pressures to flush the cell.
Note that some moored sensors (SBE 37-SIP, 37-SIP-IDO, 37-SMP, 37-SMP-IDO, 37-SMP-ODO, 37-IMP, 37-IMP-IDO, 37-IMP-ODO, HydroCAT, HydroCAT-EP) have a recommended orientation because of their u-shaped plumbing configuration. Refer to the instrument manual for details.
All Thetis models include an integrated GPS system. GPS acquisition times are typically less than 2 minutes. The GPS is only activated if a break-away condition has been detected.
There is an option to integrate an autonomous (self-contained and powered) Iridium beacon with the Thetis Profiler.
Very few Sea-Bird instruments completely fail due to component malfunction or manufacturing defects. However, we see a reasonably large number that require repairs of some sort. Most of these are simply due to the user breaking the equipment through rough handling, accidents, or lack of maintenance. It always best to plan for the worst case.
Parts most likely to be damaged are cables, connectors, and sensors (specifically the conductivity cell). Cables and connectors are easily replaced and spares should always be carried. After a sensor is replaced, the instrument must be re-calibrated, so it is really not practical to carry spare cells or temperature probes. If you start carrying many spare boards and sensors you are better off (both in cost and efficiency) having whole spare instruments on board.
Carrying at least 1 complete set of spares, with 3 sets of cables, connectors and dummy plugs, is recommended. How fast you can get spares from shore to the ship should dictate how many spare systems you need to have on board.
Note: See spares recommendations specific to the SBE 9plus.
The Thetis system uses on board batteries (BlueFin Robotics, 1.5kW) for power.
Sea-Bird’s CTDs are not directly affected by adjacent objects, unlike some CTDs that shift their calibration due to proximity effects. However, the CTD can only measure the water it sees. There are 2 concerns to keep in mind when mounting the CTD:
- If the CTD is positioned so that the flow of water is blocked or restricted, the CTD will see water that lags behind the true environment. Also, there is a directivity affect in the conductivity measurement: The instrument measures only the conductivity of the water in its conductivity cell. This conductivity cell is oriented along the long axis of the CTD, so it will work better (i.e., get flushed with water representing the true environment) if water can flow along this axis. This is accomplished by orientation of the conductivity cell parallel to the direction of movement and with the use of a pump.
- The thermal mass of adjacent objects can affect the temperature of the water. If the CTD is near some large object that takes a long time to equilibrate to changing temperature, the temperature of the water in the vicinity will be affected and the CTD will read this affected temperature.
Our current depth operating specification for the Thetis Profiler is in water columns ranging from 5 to 100m in depth. The Thetis Profiler has been most rigorously testing in 50 m offshore of Newport, OR, though other systems have been deployed in several other locations.
While a CTD leak can result in a dangerous situation, it is not common. Pressure housings may flood under pressure due to dirty or damaged o-rings, or other failed seals, causing highly compressed air to be trapped inside. For example, a housing that floods at 5000 meters depth holds an internal pressure of more than 7000 psia. If this happens, a potentially life-threatening situation can occur when the instrument is brought to the surface. The CTD will not explode. If it does flood and develop pressure inside, the end cap can be shot out of the housing if a technician tries to open the unit without releasing the pressure first.
Possible causes of flooding include:
- O-rings were not properly prepared or greased after the housing was opened, or
- Instrument was dropped or hit hard, and a bulkhead connector or the sensor was cracked or damaged.
It is important to visually inspect the instrument for damage before each survey. A cracked bulkhead connector is usually easy to spot.
If the instrument is unresponsive to commands or shows other signs of flooding or damage, see the Recovery section in your instrument manual for details specific to your instrument. For most instruments, follow these precautions:
- Every time you open the instrument, loosen each end cap screw a few turns. If the end cap follows the screws out, there is pressure in the housing.
- If pressure in the housing is indicated:
A. Point the instrument in a safe direction away from people.
B. Loosen 1 of the bulkhead connectors very slowly, at least 1 turn, to release the pressure safely (bulkhead connectors are the black connectors on the end cap, where the cables attach to the instrument). This opens an O-ring seal under the connector. Look for signs of internal pressure (hissing or water leak). If internal pressure is detected, let it bleed off slowly past the connector o-ring. Then, you can safely remove the end cap.
In general, instruments do not flood. However, be aware of the potential for flooding so that if a problem arises you will be able to safely deal with it.
It is not necessary to put the instrument in water to test it. It will not hurt the conductivity cell to be in air.
If there is a pump on the instrument, it should not be run for extended periods in air.
- Profiling instruments (SBE 9plus, 19, 19plus, 19plus V2, 25, 25plus, 49, GPCTD) and some moored instruments (all pumped MicroCATs with integral dissolved oxygen (DO), pumped MicroCATs without DO with firmware 3.0 and later, and all HydroCATs and HydroCAT-EPs) do not turn on the pump unless the conductivity frequency is above a specified minimum value (minimum value is hard-wired in 9plus, user-programmable in other instruments). This prevents the pump from turning on in air. See the instrument manual for details.
- If your instrument does not check for conductivity frequency before turning on the pump:
– For moored SeaCATs (16, 16plus, 16plus-IM, 16plus V2, 16plus-IM V2): Disconnect the pump cable for the test.
– For older pumped MicroCATs: orient the MicroCAT to provide an upright U-shape for the plumbing. Then fill the inside of the pump head with water via the pump exhaust tubing; this will provide enough lubrication to prevent pump damage during brief testing.
This topic is covered in detail on the UNOLS (University-National Oceanographic Laboratory System) website; see http://www.unols.org/publications/winch_wire_handbook__3rd_ed/06_wire_rope_em_cable_lub.PDF.
Sea-Bird typically recommends using the Dam/Blok and EverGrip products from PMI Industries. DamBlok makes the electrical splice and EverGrip provides the strain relief on the cable. See an example of how these products can be used.
For a quick electrical splice in the field using commonly available materials, the UNOLS (University-National Oceanographic Laboratory System) website provides a procedure using hot glue and heat shrink: https://www.unols.org/document/using-hot-glueheatshrink-terminations-rowe. Numerous cycles of deployment to great depths could compromise the seal, but it may be useful for a quick fix.
Digiquartz pressure sensors are used in the SBE 9plus, 53, and 54. The SBE 16plus V2, 16plus-IM V2, 19plus V2, and 26plus can be equipped with either a Druck pressure sensor or a Digiquartz pressure sensor. All other instruments that include pressure use a Druck pressure sensor.
- The overpressure rating for a Digiquartz (as stated by Paroscientific) is 1.2 * full scale. The sensor will provide data values above 100% of rated full scale; however, Sea-Bird does not calibrate beyond the rated full scale.
- The overpressure rating for a Druck (as stated by Druck) is 1.5 * full scale. The sensor will provide data values above 100% of rated full scale; however, Sea-Bird does not calibrate beyond the rated full scale.
Note: If you use the instrument above the rated range, you do so at your own risk; the product will not be covered under warranty.
Cable length is one of the most misunderstood items in the RS-232 world. The RS-232 standard was originally developed decades ago for a 19200 baud rate, and defines the maximum cable length as 50 feet, or the cable length equal to a capacitance of 2500 pF. The capacitance rule is often forgotten; using a cable with low capacitance allows you to span longer distances without going beyond the limitations of the standard. Also, the maximum cable length mentioned in the standard is based on 19200 baud rate; if baud is reduced by a factor of 2 or 4, the maximum length increases dramatically. Using typical underwater cables, allowable combinations of cable length and baud rate for Sea-Bird instruments communicating with RS-232 are shown below:
| Maximum Cable Length (meters) | Maximum Baud Rate* |
|---|---|
| 1600 | 600 |
| 800 | 1200 |
| 400 | 2400 |
| 200 | 4800 |
| 100 | 9600 |
| 50 | 19,200 |
| 25 | 38,400 |
| 16 | 57,600 |
| 8 | 115,200 |
*Note: Consult instrument manual for baud rates supported for your instrument.
First off, let’s see what a relatively good Raw Data Plot looks like.

The different phases are the pre-flush phase (dark blue), the ambient baseline reading period (red), the sample reagent pump phase (green), the sample read/reaction phase (purple), and finally the post-flush phase (dark blue). During a “spiked run” the full set of phases are repeated twice.
Using this as an example, you want to see a flat pre- and post-pump phase, a stable (flat) ambient read phase, and a pronounced smooth reaction curve. You may see small bumps here and there due to very small bubbles or other effects but this can be negligible.
The most common failure mode is the bubble spike flag, which triggers when air is introduced into the system, most commonly through the sample line but possibly through incorrectly installed cartridges or tubing.

The bubble failure is typically identified by large jumps and spikes randomly in the data, primarily in the pre- and post- pump phase and the ambient read phase. Air bubbles create an unstable base line (red) which will affect the sensor’s accuracy. In extreme examples it can completely overshadow the reaction curve as well or shift the baseline to the point where your reaction creates a negative value. Air bubbles often exacerbate other issues, like weak pumps, clogged filters, or already low phosphate in your sample.
Since bubbles can come from a few different places there are multiple checks you can do to try to stop bubbles from appearing in your data. The most important check is ensuring that your hydrocycle is fully submerged for the entirety of your deployment, as the sample line being exposed to air will introduce bubbles.
You should check that each of your reagent carts are fully installed. Press down on each reagent cart until you can hear them click and be careful about applying too much force to any of the plastic pieces that may crack and allow for leaks or air.
You can also test the pump volumes of each reagent and sample to see if your filters are clogged or if there is another issue causing the sample injection system to fail, like a leak. You do so by using Cyclehost’s Pump controls. You should choose all pumps and run each for 100 pumps. A healthy system will pump 1-1.3 ml of reagent and 2.5-3 ml of sample.
If you have bubbles already and need to recover, the most thorough method is to follow our maintenance and cleaning instructions in the manual, primarily the extended flush. Running the extended flush multiple times should be enough to clear bubbles from your system if no other issues are evident.
If doing so still fails to recover your instrument’s counts please reach out to technical support with a copy of your hydrocycle data and brief timeline of events.
Other
The SBE9/11+ system does not have the capability to support any instrumentation data or signals via its sea cable that are not directly connected to the SBE9+ CTD and associated carousels.
There is a hardware upgrade on the 9/11+ system that provides a serial RS-232 data uplink. This is a relatively constrained feature on the 9/11+ system, that allows a serial RS-232 data stream to be passed up the sea cable and saved as a separate data file.
NOTE: This upgrade is installed in the 9/11+ at the factory and operates at 9600 baud, requiring
that the 9/11+ be configured/operating at this same baud rate.
None of this is compatible with a video signal to be integrated into this system. Additional hardware components inline with the sea cable that are not supplied by Sea-Bird Scientific would be required. This custom application is not currently supported.
Sea-bird Scientific no longer directly sells and ships Triton-X. Since January 4th,2021 Triton-X has been banned in the EU due to a key ingredient being a known endocrine disrupter. TERGITOL is a non-ionic surfactant which can be used as a substitute for Triton-X. It can be purchased at Sigma Aldrich. The surfactant is supplied in 100% strength and will need to be diluted. If neither surfactant is available, vinegar or a diluted bleach solution can be used as a substitute.
- Conductivity sensors — TERGITOL is typically diluted to 0.1% strength (by 1000) for rinsing and for rewetting the conductivity cell just before deployment, and to 1% to 2% strength (by 50 to 100) for cleaning the conductivity cell. Refer to Application Note 2D: Instructions for Care and Cleaning of Conductivity Cells and to the maintenance section in the instrument manual for details.
- SBE 43 (membrane-type) Dissolved Oxygen sensors — TERGITOL is typically diluted to 0.1% strength (by 1000) for rinsing, and to 1% (by 100) for cleaning. Prolonged exposure of the sensor membrane to Triton causes the sensor’s calibration to drift. Do not place Triton directly on the membrane. See Application Note 64: SBE 43 Dissolved Oxygen Sensor – Background Information, Deployment Recommendations, and Cleaning and Storage for details.
- SBE 63 Optical Dissolved Oxygen sensors — TERGITOL is typically diluted to 0.1% strength (by 1000) for rinsing, and to 1% (by 100) for cleaning. Do not place TERGITOL directly on the optical window. See the SBE 63 manual for details.
This is a safety feature of the instrument, whereby the lamp is turned off when its temperature reaches 35°C (95°F) to prevent damage from overheating. The SUNA continues to output dark frames while monitoring the temperature, and will restart the lamp once it has dropped back below 35°C. If extended in-lab use is required, immersing the SUNA in a cool bath can prevent this behavior.
The most common telemetry system utilized is a FreeWave radio system. Transmission times for the science data are typically 20-30 seconds through the FreeWave modem when the receiver is within 3 km of the profiler.
Other telemetry systems include a broadband cellular and Iridium modems.
Recent FAQs
Software & Data Processing
The deep SBE41 and SBE61 use the same pressure sensor – a 7000dbar Kistler. And, they are calibrated with the same Paroscientific Digiquartz reference. However, the calibration process is different. A deep SBE41 receives a 2-point sensor only temperature compensation for pressure. The initial accuracy for a deep 41 is +/- 7dbar, typical stability is 2dbar/year. A 61 receives a 4-point temperature compensation for pressure after the instrument is completely assembled, such that the correction includes both the sensor and the electronic boards. The initial accuracy for a 61 is +/-4.5dbar, typical stability is 0.8dbar/year.
The menu to configure the factory parameters you are asking about is accessible through the i*? command. The ? argument for this command will give you a list of all of the arguments to change each individual menu. Let me know if you have any questions about the list of commands in the help menu, and I can try to clarify.
Some cautionary suggestions about changing these parameters:
(1) These parameters should only be changed prior to deployment. Changing them post-deployment could cause you to permanently lose your ability to communicate with the float remotely.
(2) In order to retain Sea-bird Navis warranty coverage, you must provide a log of pre-deployment testing that includes telemetry to your server system after all parameter updates have been performed.
Scientific
The deep SBE41 and SBE61 use the same pressure sensor – a 7000dbar Kistler. And, they are calibrated with the same Paroscientific Digiquartz reference. However, the calibration process is different. A deep SBE41 receives a 2-point sensor only temperature compensation for pressure. The initial accuracy for a deep 41 is +/- 7dbar, typical stability is 2dbar/year. A 61 receives a 4-point temperature compensation for pressure after the instrument is completely assembled, such that the correction includes both the sensor and the electronic boards. The initial accuracy for a 61 is +/-4.5dbar, typical stability is 0.8dbar/year.
Field Procedures & Deployment
The SUNA V2 has capacitors that maintain internal power for to the electronics long enough for a proper shutdown process when external power is removed. However, these capacitors must completely discharge between power cycles, or else the SUNA may fail to properly boot up when external power is reapplied. If your SUNA is stuck in a state where it will not respond to external power, unplug the bulkhead connector completely from the SUNA and wait 30-60 seconds before reapplying external power again.